물리식의 의미에 대한 분석 : 존재론 차원과 인식론 차원을 중심으로

Vol. 66, No. 1, January 2016, pp. 50∼60 http://dx.doi.org/10.3938/NPSM.66.50

An Analysis of the Meanings of Physics Equations with a Focus on the Ontological and Epistemological Dimensions

Minchul Kim · Yongwook Cheong · Jinwoong Song

Department of Physics Education, Seoul National University, Seoul 08826, Korea (Received 15 October 2015 : revised 3 November 2015 : accepted 4 November 2015)

A physics equation is a symbolic representation of physics knowledge through mathematical mod- eling. The equation is a medium that links physics with mathematics, making necessary a teaching and learning approach in which physics equations can be used to provide a way of understanding physics concepts beyond their use as a simple tool of physics problem solving. This study provides a hierarchical analysis at three levels on the meanings of physics equations. In the process, the difference between physics equations and mathematics formulae, and the difference between the physical meanings and the mathematical meanings of physics equations are analyzed. In particular, the physical meanings of the equations are analyzed and synthesized in ontological and epistemo- logical dimensions. The framework and the results of this study may provide a foundation for more meaningful teaching and learning of physics equations.

PACS numbers: 01.40.E-

Keywords: Physics equation, Physical meaning, Mathematical meaning, Ontological category, Epistemolog- ical category

물리식의 의미에 대한 분석 : 존재론 차원과 인식론 차원을 중심으로

김민철 · 정용욱 · 송진웅

서울대학교 사범대학 물리교육과, 서울 08826, 대한민국

(2015년 10월 15일 받음, 2015년 11월 3일 수정본 받음, 2015년 11월 4일 게재 확정)

물리식은 물리 개념에 대한 지식을 수학적으로 모델링하여 기호들의 관계로 나타낸 것이다. 물리식은 물리와 수학을 연결하는 매개체이기 때문에 물리식을 단순히 문제풀이의 수단으로서가 아닌 물리 개념을 이해하기 위한 수단이 되도록 하는 교수학습이 필요하다. 이를 위해 본 연구는 물리식이 갖는 의미에 대해 세 수준의 위계적인 분석을 수행하였다. 이 과정에서 물리식과 수학식의 차이점, 물리식에 대한 물리적 의미와 수학적 의미의 차이점을 분석하였다. 특히 식의 물리적 의미를 존재론적 범주차원과 인식론적 범주차원에서 분석하고 이를 종합하였다. 본 연구에서 제시하는 분석틀과 분석결과는 물리식에 대한 보다 유의미한 교수학습을 위한 토대를 제공할 수 있을 것이다.

PACS numbers: 01.40.E-

Keywords: 물리식, 물리적 의미, 수학적 의미, 존재론적 범주, 인식론적 범주

∗E-mail: jwsong@snu.ac.kr

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

I. 서 론

물리식은 물리 개념을 정의하고 물리에 관한 원리와 법칙을 담아내는 등의 개념적 지식을 수학적으로 모델링 (modeling) 하여 기호들의 관계로 간단하게 표시한 것이 다. 물리식은 물리와 수학을 연계하는 매개체이며 물리 법칙이나 원리를 문제해결에 이용할 수 있게 해주는 역할을 한다. 그러므로 물리식은 문제풀이에 맥락화시킴으로써 물리 법칙과 원리를 잘 이해 할 수 있게 해주는 도구도 된다.

이런 의미에서 물리식은 개념지식 (conceptual knowledge) 과 과정지식 (procedural knowledge) 을 연결시켜주는 매 개체라고 할 수 있다. 그러나 물리식에 대한 통상적인 교 수학습에서 물리식의 개념적 차원에 관한 학습과 물리식을 문제풀이에 이용하는 방법과 관련된 절차적 차원에 관한 학습은 조화를 이루지 못하는 모습을 보이기 쉽다 [1].

수학은 단지 계산을 위한 도구이며 종종 물리학의 개념 이해를 방해하는 것으로 여겨지기도 하지만 사회적, 인식론 적, 존재론적으로 물리의 수학화는 효과적인 측면이 크다 [2]. 물리이론의 역사적 발전을 추적해보면 물리학자들이 직관적 물리 원리로부터 연구를 시작하여 수학적 구조의 탐색으로 연구를 확장하는 경우를 다수 확인할 수 있다 [3].

이를테면 아인슈타인은 물리학에 내재된 수학적 성격을 강조한 물리학자 중 하나이다 [4]. 물리 개념을 이해하기 위해서 수학에 대한 이해는 매우 중요하며 그런 의미에서 물리식에 담긴 다양한 의미를 설명하는 것은 물리식에 대한 이해에 있어서 매우 중요하다고 할 수 있다.

Kragh [5]는 물리와 수학의 상호작용은 역사적으로 매우 다양하였고 이러한 복합적인 상호작용을 교수학습과정에 서 학생들과 논의해야 한다고 주장하였다. Kjeldsen 와 Lutzen [6]은 물리학에 기원을 둔 수학적 개념에 관한 수학 의 본성 (nature of mathematics) 을 탐색한 연구를 통해 함 수 (function) 를 정의하는 역사적 과정에서 물리학의 영향 (운동학, 진동하는 줄, 열전도, 전기역학, 양자역학) 을 강조 하였다. 한편으로 아인슈타인이 플랑크의 복사 법칙의 물리 적 내용을 명확하게 하는 과정에서 잘 알려진 물리 체계에 대한 방정식과 잘 이해되지 않는 물리 체계에 대한 방정식의 통사적 형태를 비교하는 형식적 유추 (formal analogis) 를 사용한 것에서 보듯이 물리학과 수학은 매우 상호 의존적 이라고 할 수 있다 [7]. 이러한 상호의존성에도 불구하고 대체로 물리 교육에서는 수학을 단지 계산 (calculation) 과 서술 (description) 을 위한 도구로 보며, 수학 교육에서는 물리를 추상적으로 정의된 수학적 개념을 응용할 수 있는 맥락 (context) 으로만 본다. 결국 교육 현장에서는 물리학 과 수학 사이의 다양한 상호작용을 놓치고 있으며 심지어는

물리학에서 수학적인 면이 지나치게 강조되기도 하는 것 또한 현실이다.

물리 개념 연구들은 물리식을 물리 문제 풀이에의 도구 로 보는 관점에 머물고 있기 때문에 물리식이 담고 있는 중요하고 다양한 기본적인 개념을 놓치기 쉽다 [8]. 또한, Arons [9]는 판에 박히고 융통성 없는 사례를 갖고 숫자를 대입하는 문제들을 잔뜩 풀게 하는 교육은 현상적인 사고나 추리의 부족을 낳으면서 매우 심각한 불균형을 유발한다고 주장하였다. 또한 물리식을 찾고 조작하는 것에 익숙한 학 생들도 여전히 물리 개념이나 원리에 대하여 많은 오개념을 갖고 있다. 물리적 이해나 직관은 많은 문제를 푼다고 해서 저절로 얻어지는 것이 아니다 [1]. 따라서 효과적인 물리 개 념학습을 위해서 교수학습 상의 적절한 순서와 위계 구축이 필요하다. 이를테면 물리 학습은 정성적 (qualitative) 개념 이해로부터 시작하여 정량적인 (quantitative) 수준으로 천천히 진행되어야 한다 [4]. 그럼에도 불구하고, 많은 물리 교재에서 제시된 물리식들은 그것을 구성하는 개념들 간의 의미관계, 물리 이론에서의 역할, 그것이 전제하는 많은 가정들과 제한 사항을 무시한 채 문제풀이를 위한 수학적 도구로 이용되고 있다. 또한, 학생들은 물리 학습 상황에서 수치 조작과 대입을 통해 식을 나열하고 예제를 모방하는 경향을 가지며, 활용할 공식을 먼저 찾고 보는 편중된 문제 풀이 (formula-centered problem-solving) 전략을 쉽게 버 리지 못한다 [10].

이러한 문제의식에서 과제나 시험문제들이 단순히 식을 찾고 (formula-seeking apporach), 조작하여 (symbol ma- nipulation) 수치 (number) 를 얻는 접근 방식을 지양하고 물리 현상에 대한 개념적이고 정성적인 분석을 요구하여 과학적 추론을 강조해야 한다는 지적이 있다 [1]. 또한, 물리 식의 다양한 의미에 대한 이해는 과학 지식의 잠정성, 과학 적 이론, 과학적 법칙, 이론과 법칙의 관계, 이론과 실험의 특징과 상호작용 등의 과학의 본성에 대한 이해와 연관되어 있다 [11].

물리식에 대한 수학적 역할이 과연 도구적 차원에 제한 되는지를 탐색한 연구에서는 절차적 지식으로서의 물리식 의 의미를 넘어서는 물리식의 또 다른 의미와 역할을 제시 하고 있다 [12,13]. 이를테면 Brush [12]는 물리학습에서 수학의 긍정적인 역할에 대한 에피소드를 통해 물리에서 수학의 역할이 단지 계산을 위한 도구가 아님을 주장하였 다. 그는 미적분학을 물리식의 유도나 적분을 위한 도구로 제한적으로 사용하는 것은 물리학에서 미적분학을 의미 있게 사용하는 방식의 학습, 즉 물리적 상황의 수학화를 방해한다고 보았다. Gay 등 [13]은 수학의 엄격한 적용과 물리적 직관 사이의 이분법적 사고가 만연해 있지만 수학의 엄격한 적용이 물리적 상황을 모델링하는 데 도움이 된다고

주장하였다. 또한 Kneubil과 Robilotta [14]는 물리적 세계 에 대한 인식론적 추론 도구로서 수학의 사용을 가르치기 위해 “물리식의 변수 간 연결은 어떻게 되어 있는가?”, “왜 물리식은 특별한 구조를 갖고 있는가?” 등의 다양한 종류의 질문을 해야 한다고 주장하였다.

Redish와 Kuo [15]는 수학을 잘 하는 학생들도 물리에 서 수학을 사용할 때 어려움을 겪는 이유를 두 학문이 사 용하는 언어의 차이 (language difference) 때문으로 보았 다. 그들에 의하면 이러한 문제는 수학 수업을 추가로 실 시한다고 해결되지 않으며 물리적 상황을 수식화하는 능 력을 포함하여 물리적 의미 (physical meaning) 와 수학적 구조 (mathematical structure) 를 융합하는 교수학습을 통 해서 해결할 수 있다. 한편 Karam과 Krey [16]는 물리식 의 학습 상황에서 숫자를 대입하면 답이 나오는 plug-and- chug 방식을 극복하기 위하여 단순한 계산 (caldulation) 과 서술 (description) 로부터 설명 (explaination) 과 이해 (understanding) 로의 변화를 추구해야 한다고 보았다. 이 와 같이 여러 연구자들은 물리식의 다양한 의미에 대한 이해 를 위해 수학적 구조뿐만 아니라 물리적 의미도 중요하다는 것을 지적하고 있다. 즉, 물리식에 대한 수학적 구조에 대한 설명만으로 그 물리식이 의미하는 것을 잘 설명하였다고 할 수 없다는 것이다.

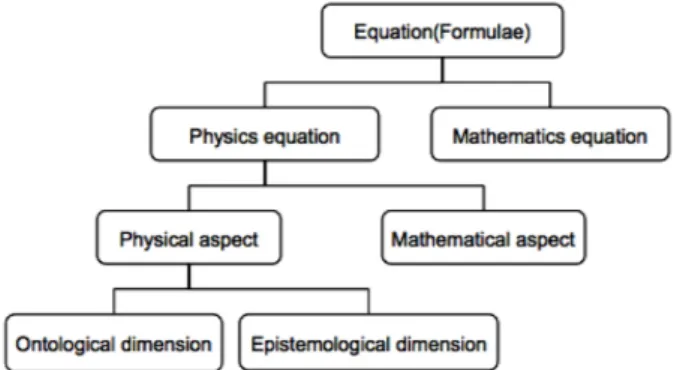
앞서 살펴본 바와 같이 여러 선행연구에서 물리식의 수학 적 의미 및 물리적 의미와 관련된 교수학습 상의 쟁점들을 다루었다. 또한 상당수 연구는 수학적 의미보다 물리적 의미를 강조하는 교수학습의 필요성을 지적하고 있다. 그 런데 물리학 교수학습에서 수학적 의미와 구별되는 물리적 의미란 무엇인지를 명료하게 규정한 연구는 드물다. 이러 한 문제의식에서 본 연구는 물리식이 갖는 물리적 의미를 명료화하는 작업을 진행하였다. 이를 위해 Fig. 1과 같이 물리식과 수학식을 구별하고, 물리식의 수학적 측면의 설 명과 물리적 측면의 설명을 구별하였다. 또한, 물리식의 물리적 측면의 설명을 식에 포함된 개념들 간의 관계를 규정하는 ‘존재론적 범주’ 차원과 물리 이론에서 물리식의 역할에 대한 ‘인식론적 범주’ 차원으로 구분하여 물리식이 갖는 의미를 정리함으로써 물리학의 교수학습을 위한 기초 토대를 제시하고자 한다.

II. 물리식과 수학식

물리학에서 사용하는 공식은 수학에서 사용하는 식과는 몇 가지 다른 점을 갖는다. 첫째, 수학은 물리적인 면이 무시되는 추상적인 것과 이상적 상황을 다루기 때문에 정 확하다고 할 수 있다 [17]. 반면에 물리학은 실제 현상을

Fig. 1. Hierarchical classification of meaning of physics equation.

이상적 상황으로 해석하기 때문에 맥락을 고려해야 한다는 점이 수학과 다르다. 그러므로 물리식이 가정 사항이나 성립 조건 및 한계점 때문에 모든 상황에 항상 적용할 수 없는 반면, 수학식은 항상 적용할 수 있으며 언제나 옳다고 할 수 있다. 이런 의미에서 물리식은 맥락적이어서 상황에 따라 옳거나 옳지 않을 수 있다. 둘째, 물리식은 식을 구성 하는 각각의 기호들에 대한 대상체가 있는 반면, 수학식은 대상체가 없다. 즉, 힘, 질량, 가속도 등은 추상적이든 구체 적이든 그것이 의미하는 대상물이 있다. 하지만, 수학식이 포함하는 각각의 기호는 단지 수 (number) 와 추상적 규약 을 나타낸다 [15].

학습과정에서 물리식과 수학식의 이러한 차이를 학습자가 인식할 필요가 있다. 그렇지만 Redish와 Kuo [15]의 연구에 서 보듯이 학생들은 이러한 차이를 놓치기 쉽다. 그들은 학 생들에게 숨은 전하들에 의해 만들어진 전기장 속에서 크기 가 매우 작은 시험 전하 (test charge) q 가 받는 힘을 F , 시험 전하가 받는 전기장의 세기 E = F /q 라고 제시하면서 전하 q를−3q 로 바꾸면 전기장의 세기는 어떻게 되는지 물었다.

그들의 연구에 참여한 200여명의 학생 중 100명이 넘는 학 생들이−E/3를 정답으로 선택하였다. 이러한 결과는 학생 들이 전기장을 나타내는 식 E = F /q 를 비례관계를 나타내 는 수학적 문법 (mathematical grammar) 으로 해석하여 전 하가 -3배가 되니까 전기장은 -1/3배 (F /(−3q) = −E/3) 가 된다고 생각하였기 때문이라고 해석되었다. 이와 같이 학생들은 전기장의 세기가 시험 전하 (test charge) 와 독립 적이라는 물리적 상황을 무시하고 물리식을 수학식이 갖고 있는 문법대로 다루는 경향을 보였다.

물리식은 이전 물리학 연구의 결과이자 물리적 직관의 표현이라 할 수 있다. 부르너의 표현 양식 중 상징적 표상에 해당하는 물리식은 과학이 수학, 철학, 역사, 언어 모두와 관계를 맺고 있음을 나타낸다. 과학사적인 면에서 살펴보면 고대에는 수식 대신에 주로 기하학을 이용하여 과학적인 법칙이나 원리를 나타내었다. 그럼에도 불구하고 일부 식의

형태를 볼 수 있는데, 이를테면 4세기 경 Pappus는 경사면 에서의 운동에 관한 이론을 설명하면서 식의 형식를 사용하 였다 [18]. 이후 식의 사용은 중세까지는 활발하지 않다가 미적분학 발견을 계기로 식을 활용한 수학적 체계화 과정이 강화되었다 [19]. 역학에서 시작된 식의 체계화는 이후에 전자기학 등 물리학의 다른 분야로 전파되었다. 이후에 오 일러, 라그랑지, 라플라스의 연구를 통해 오늘날 통용되는 것과 유사한 형태의 법칙의 수식화가 이루어졌다 [18].

이러한 수식화를 통해 역학적 아이디어를 다루는 데 있 어서 발전을 이룰 수 있었다. 현대 물리에 와서는 기하 (geometry) 의 사용이 줄어들었고 식은 더욱 빈번히 사용되 었다. 이는 우리의 관심이 연속체 단위 (continuum scale) 에서 원자 단위 (atomic scale) 로 변화되면서 나타나는 자연 스러운 결과라고 할 수 있다 [20]. 이처럼 물리식은 그것을 나타내는 형식과 의미면에서 진화되었다.

물리현상과 관련된 법칙이나 원리, 물리적인 개념에 대 한 정의들이 모두 공식으로 표현되는 것은 아니지만 많은 중요한 물리학 아이디어들은 물리식으로 표현될 수 있다.

그러므로 물리를 배우는 학생들이 물리현상을 이해하기 위 하여 법칙이나 원리를 표현한 물리식을 접하는 것은 당연한 일이다. 또한, 수학적 구조의 사용과 물리적 실재의 연결은 물리학 교수학습에서도 바람직하다 [21].

물리식은 물리적 개념을 나타내는 기호를 담고 있으며, 물리 개념 간의 관계를 나타내고 있다 [22]. 이러한 기호는 물리적 개념을 나타내는 기호 (예 : F, E, m 등) 와 개념간의 관계를 나타내는 수학적 연산을 의미하는 기호 (예 : +,−,

×, ÷, =, ∑ , √

, d/dt, ∫

등) 로 나눌 수 있다. 또한, 각 각의 기호는 상수 (constant), 파라미터 (parameter), 변수 (variables) 로 나눌 수 있다 [23]. 여기서 상수 (constant) 는 변하지 않는 수학적, 물리적 양으로 1/2이나 3과 같은 분수나 정수, e 나 π 와 같은 명명된 숫자 (named number), G나ℏ와 같은 물리적 상수 (physcal constant)로 나눌 수 있다. 파라미터 (parameter) 는 특별한 상황이나 실험세팅 에서 변하지 않지만, 상황이나 실험세팅이 달라지면 변화 되는 상황적 상수이다. 변수 (variables) 는 그 상황에서의 독립변인과 종속변인을 나타낸다.

물리식에서의 수학적 연산 기호의 의미는 Sherin [8]의 연구에서 기호 형태 (symbolic form) 로 설명되었다. 예를 들면 그는 등호 (=) 의 의미를 계의 평형 상태를 나타내는 평형 (balancing), 등호 양쪽의 양이 같음을 나타내는 동일 양 (same amount), 등호 왼쪽에 하나의 기호만을 표시하는 규정 (identity) 으로 구분하였다. 또한 덧셈의 기호 (+) 를 a(t) = −g + f(v)/m 과 같이 중력과 공기저항력에 의한 경쟁적이고 반대적인 의미를 나타내는 경쟁항 (competing terms), 전체의 일부 (parts of a whole), 기준치와 변화량

(base+change) 의 의미로 구분하여 설명하였다. 하지만 이 러한 구분만으로 물리식의 의미를 충분히 논의하기 힘들다.

이를테면H −→

B d⃗l = µ₀ϵ₀dΦ_E/dt + µ₀I_enc (암페어-맥스웰 방정식)을 살펴보면, Sherin [8]의 연구 결과인 평형, 동일양, 규정의 의미구분 만으로 등호 (=) 의 의미를 설명하기에는 무리가 있다. 왜냐하면, 이 식은 전류나 변위전류가 원인이 되어 자기장이 만들어진다는 인과적 의미를 물리적으로 내포하고 있기 때문이다.

III. 물리식이 갖는 다차원적인 의미

앞서 논의한 Sherin의 틀이 갖는 한계는 물리식의 의미에 대한 보다 심층적인 분석의 필요성을 제기한다. 이러한 문제인식에서 본 연구는 물리식의 의미에 대한 보다 분석 적인 탐색을 수행하였다. 그 결과로 물리식의 수학적 의미 와 물리적 의미를 구분하고, 물리적 의미를 다시 존재론적 차원과 인식론적 차원으로 구분하는 다차원적인 탐색을 수행하였다.

1. 물리식의 수학적 의미

본 연구는 물리식에 대한 수학적 서술과 물리적 서술을 구별하고자 한다. 식에 대한 수학적 서술은 수학이 물리식에 대하여 구문론 (syntax) 을 제공하여 기호들의 수량관계와 연산관계에 대하여 알려주는 것이고, 물리적 설명은 물리 식에 대하여 의미론 (semantic) 을 제공하여 기호들과 그것 들이 적용되는 개체간의 관계에 대하여 알려주어 물리적 해석을 가능하게 해준다. 많은 교재에서 뉴턴의 2법칙을 표현하는 식 F = ma 에 대해 “어떤 물체에 가한 알짜힘은 그 물체의 질량과 가속도의 곱이다. [24]” 또는 “물체의 가속도는 그 물체에 작용하는 알짜힘에 비례하고 질량에 반비례한다 [25,26].” 라는 식의 서술을 발견할 수 있다. 전 기장에 대한 가우스 법칙을 나타내는 식HE⃗·d ⃗A = q_enc/ϵ₀ 에 대해서는 “폐곡면을 통과하는 전기장에 대한 면적분은 그면 내부에 있는 알짜 전하량을 ϵ0로 나누어 준 값과 같다.

[27,28]” 라는 식의 서술을 볼 수 있다. 물리식에 대한 위와 같은 서술은 본 연구의 물리식의 의미 구분을 따른다면 물리적 서술보다는 수학적 서술에 가까운 것이다. 이러한 서술은 그 자체의 의미를 가지지만, 학생들에게 정성적인 이해를 제공하기 어려우므로, 식에 대한 수학적 서술 혹은 정량적 서술은 식에 대한 물리적 (정성적) 의미서술을 통 해 보강되어야 한다. 이를테면 식 F = ma 에 대해 “어떤 물체는 그 물체에 가해지는 힘에 의해 가속도가 생긴다.”

또는 “어떤 물체의 운동의 변화는 힘으로부터 기인된다.”

라는 물리적 의미를, 전기장에 대한 가우스 법칙에 대해

“전기장의 발생 원인은 전하이다.” 또는 “전하 주변에는 전기장이 발생한다.” 라는 물리적인 의미를 소개해야 한다.

그런데 영향력있는 일반물리학 교재에서 [24,27,28] 힘이나 전기장에 대한 정의로 물리적 의미 서술 대신에 수학적 의미 서술을 제시하고 있다는 것에서 볼 수 있듯이 교재에서도 물리적 의미가 수학적 의미에 비해 소홀히 다루어지는 측 면이 있다.

그런데 물리식의 의미와 관련하여 수학적 차원의 강조는 단순히 교재만의 문제가 아니며, 과학사적 근원을 갖는 문제 이다. 이를테면 뉴턴은 Principia에서 “나는 단지 그런 힘을 수학적 개념으로 설명하려는 것일 뿐이다. 물리적 원인과 배경이 무엇인가는 고려하지 않는다. 나는 중심을 향하는 일종의 인력, 충격, 혹은 경향이라는 말을 서로 뒤섞어 사용 하며 다르지 않게 쓴다. 힘을 물리적으로 생각하기보다는 수학적으로 생각한다.” 라고 하였다. 뉴턴 이후로 물리에서 수학의 역할은 매우 커졌지만, 이러한 수학의 역할강화에 모두가 찬성한 것은 아니었다. 이를테면 패러데이는 당시의 전자기학의 수학화에 대하여 회의적이었다. 그러나 맥스 웰이 다시 양에 관련된 법칙은 정확한 추론 원리에 맞게 다루어져야 하기 때문에 자연철학은 수학이어야 한다고 주장하는 등 대체로 페러데이 등의 반대는 잊혀졌다.

물리의 수학화로 인해 사회적인 측면에서 많은 관련자 들이 자연철학에 대한 담화에의 참여로부터 배제되었다.

인식론적인 측면에서는 운동학에서 사용되던 수학과는 다 르게 역학에서 수학이 사용됨으로써 ‘설명 (explanation)’

의 의미가 변화되었으며, 존재론적인 측면에서는 현상에 대한 더 많은 추상화로 인해 물질 (substances) 이 사라지게 되었다 [7]. 이러한 변화에 대해 물리는 ‘역학적 설명’ 을 제공해야 하며 이것과 ‘수학적 설명’ 을 혼동하지 말아야 한다는 주장도 있다 [7]. 이러한 입장에서는 수학적 설명 과 물리적 설명은 상호의존적이지만 Principia에서 뉴턴 이 물리적 현상을 수학적 언어로 설명한 이래로 구체적인

‘물리적 설명’ 과 추상적인 ‘수학적 설명’ 은 혼용되었고,

‘물리적 설명’ 없이 물리와 수학을 융합하기 때문에 물리는 더 이상 이해하기 쉽지 않게 되었다고 본다. 이러한 혼용은 현재 우리 과학교육의 현장과도 무관하지 않다. 학생들에게 물리식에 대한 수학적 설명이 강조된다면 학생들이 식에 대한 직관적이고 물리적인 의미를 찾는 것은 상당히 어려운 과업일 수 있다. 학생들이 수학적 과정 상의 어려움으로 물리적인 의미를 찾기도 전에 물리 학습을 포기하는 상황도 배제할 수 없다.

2. 물리식의 물리적 의미 1:�존재론적 차원

오늘날 과학교육과정은 단순히 과학자 양성을 넘어서서 과학적 소양의 함양을 표방하며, 이를 위해서 과학의 본성에 대한 이해가 중요하게 여겨진다 [11]. 물리식에 관한 학습도 이러한 시대적 요구를 반영할 필요가 있다. 즉 물리식을 교수학습에서 다룰 때 과학지식의 잠정성, 이론과 법칙의 관계와 작용, 과학적 방법, 과학적 이론, 과학적 법칙, 과학 자의 역할, 과학지식의 인식론적 지위 등의 과학의 본성과 관련한 논의를 포함하는 것을 고려할 수 있다. 특히 물리 식이 만들어진 과정이나 물리식의 물리이론에서의 역할에 대한 학습을 통해 식에 담긴 물리적 의미를 학습하는 것이 의미 있을 것이다. 이러한 인식하에 앞으로의 논의에서는 물리식의 물리적 의미를 보다 명료화하기 위한 작업으로 물리식이 담고 있는 각 개념들 사이의 관계에 관련된 존재 론적인 범주차원과 물리이론에서 물리식의 역할과 관련된 인식론적인 범주차원으로 나누어 물리식의 의미를 살펴보 고자 한다.

물리 법칙, 원리, 정의의 수학적 표현인 물리식은 물리적 개념을 나타내는 많은 기호와 수학적 연산 기호로 구성되어 있는 복합적인 학습주제이다. 이러한 물리 관계식에 대한 교수학습의 개선을 탐색할 때 물리 개념을 존재론적 범주의 차원에서 분석하는 것이 도움을 줄 수 있다는 것이 본 연구 의 입장이다. 물리 개념에 관한 존재론적 범주화 및 분류는 물리교육의 재구조화를 시도한 여러 연구자들에 의해 수 행되었다 [9,29]. 이를테면 Arons [9]는 계 (system), 속성 (property), 상호작용 (interaction) 이라는 존재론적 범주 차원의 분류를 바탕으로 에너지 보존의 교수학습방안을 논 의하였다. 한편으로 Chi [29]는 존재론적 범주와 관련된 영 향력있는 개념변화이론을 제안하면서 물질 (matter), 과정 (process) 등의 존재론적 범주를 구분하였고 때때로 속성 (property) 과 상호작용 (interaction) 의 구분을 논하기도 하였다.

이러한 존재론적 범주의 구분은 힘, 열과 같은 근본적인 물리학 개념을 이해할 때 중요할 수 있다. 이를테면 힘, 열과 관련하여 많은 학생들이 이들 개념들을 상호작용이 아닌 속성으로 취급하는 오개념을 갖고 있다는 것이 잘 알려져 있다 [29]. 이러한 사례들에서 보듯이 존재론적 범주에 대한 이해는 물리학의 개념학습에서 중요한 요소일 수 있다. 본 연구에서 말하는 식이 갖는 물리적 의미의 존재론적 차원은 바로 존재론적 범주와 관련된 물리식의 의미를 말한다.

Halloun [30]도 모형기반 물리학교수학습을 제시하면서 물리적 개념에 대한 존재론적 범주구분을 중요한 바탕으 로 삼았다. 그는 역학 학습의 맥락에서 물리식을 상태법칙 (state laws)을 나타내는 방정식, 상호작용법칙 (interaction

laws)을 나타내는 방정식, 인과법칙 (causal laws)을 나타내 는 방정식으로 구분하였다. 여기서 상태법칙은 위치, 속도, 가속도와 같은 물리적 객체 (object) 와 관련된 상태기술자 (state descriptor) 의 변화를 나타내는 것이다. 상태법칙은 패턴에 대한 기술과 관련되며, 그것의 예로는 v = v0+ at을 들 수 있다. 상호작용법칙은 상호작용하는 물체에 관련된 힘 (F) 과 같은 상호작용기술자 (interaction descriptor) 를 사용하여 나타낸다. 고전역학에서 상호작용법칙의 예로 는 뉴턴의 만유인력 법칙, 쿨롱 법칙, 탄성과 관련된 훅의 법칙이 있다. Halloun은 만유인력 법칙에서의 질량, 쿨롱 법칙에서의 전하, 훅의 법칙에서의 용수철 상수와 같은 고 유기술자 (intrinsic descriptor) 와 만유인력 법칙과 쿨롱 법칙에서의 거리, 훅의 법칙에서의 변위와 같은 상태기술자 (state descriptor) 를 구분하였다. 한편 Halloun의 인과 법 칙은 단지 패턴을 “기술 (description)” 하는 상태법칙과는 다르게 패턴에 관한 “설명 (explanation)” 과 관련이 있다.

다시 말하면, 원인을 나타내는 상호작용기술자와 결과를 나타내는 상태기술자 사이의 인과관계를 포함함으로써 인 과 법칙은 왜 그렇게 운동하는지 설명해 준다. 인과법칙의 예로는 힘이라는 상호작용기술자가 원인이 되어 운동량이 라는 상태기술자의 변화를 결과로 나타내는 뉴턴 2법칙, 일 (work) 이라는 상호작용기술자가 원인이 되어 운동에너지 라는 상태기술자가 어떻게 변하는지를 나타내는 일-에너지 정리가 있다 [30].

Etkina [31] 등도 모델링에 기반한 물리학 교수학습방안 을 제시하는 과정에서 일종의 존재론적 범주 구분을 받아 들였다. 그들은 객체 (object), 상호작용 (interaction), 계 (system), 과정 (process) 이라는 존재론적 범주에 초점을 맞추어 물리적 현상을 모델링하는 과정에서 물리학에서 다루는 관계식을 상호작용방정식 (interaction equation) 과 과정방정식 (process equation) 으로 구분하였고, 과정 방정식은 다시 상태방정식 (state equation) 과 인과방정식 (causal equation) 으로 분류하였다. 여기서, 상호작용방정 식은 객체들 (objects) 사이의 관계를 묘사하는 관계식이고, 과정방정식은 계에서의 변화를 묘사하는 관계식으로 하나의 계 안에서 객체들 (objects) 또는 서로 다른 계에서의 객체들 사이의 상호작용에 의해 나타나게 된다. 그리고 상태방정 식 (state equation) 은 하나의 계 (single system) 의 하나 이상의 속성들이 서로의 관계속에서 어떻게 변화하는지를 묘사해준다. 즉, 상태방정식은 하나의 계의 다양한 속성들 에 대응하는 각각의 양 (quantity) 사이의 정량적 관계를 수학적 표현으로 나타낸 것으로 변화의 원인에 대해서는 명시하지 않는다. 반면에 인과방정식은 계의 속성들이 환 경과의 상호작용에 의해 어떻게 영향을 받는지 묘사해준다.

그러므로 인과방정식은 계 (system) 와 환경 (environment)

사이의 물리적 상호작용에 대응하는 양들 (quantities) 을 포함하는 수학적 표현이다.

이상과 같이 존재론적 범주에 바탕하여 물리 관계식을 범주화하는 것은 물리교수학습의 재구조화를 돕는 의미있 는 작업이라 판단된다. 물리 관계식의 이해를 위해 물리 식이 갖고 있는 각각의 물리 개념들이 어떤 의미를 갖고 다른 개념들과 어떤 관계를 갖는지를 아는 것이 중요하기 때문이다. 따라서 본 연구는 기존의 분류들을 종합하여 다음과 같이 정리하고자 한다. 먼저 본 연구는 기본적으로 Etkina 등의 관계식 분류를 따르되, 그들의 일부 실수를 보완하고자 한다. Etkina [31]는 명시적으로 객체, 상호작 용, 계, 과정의 네 범주를 구분하며, 속성을 별도의 범주로 명시적으로 취급하지 않고 있다. 역학학습에서 상호작용인 힘과 속성인 에너지의 구분이 학생에게는 중요한 개념적 도전이라는 것을 고려하면 존재론적 범주체계가 속성범주 를 명시적으로 구분하는 것이 필요하다는 것이 본 연구의 입장이다. 그런데 Etkina [31] 등은 퍼텐셜에너지를 상호 작용으로 취급함으로써 속성과 상호작용의 구분에 대한 그들의 부주의를 드러내기도 하였다. 이에 대한 고려에서, 본 연구는 Etkina와 다르게 존재론적 범주체계를 설정하여 계와 객체를 구분하지 않고 과정 범주 대신에 속성 범주를 추가하여 계, 속성, 상호작용의 범주를 구분하고자 한다.

본 연구에서 계 (system) 는 입자, 이상기체 등과 같이 객체 (object) 나 객체의 집합을 나타낸다. 속성 (property) 은 질량, 운동량, 에너지 등과 같이 특정 계 (system) 에 속하는 물리량을 나타낸다. 상호작용 (interaction) 은 힘, 충격량, 일, 열 등과 같이 한 계에 속하지 않고 둘 이상의 계들 사 이에서 걸쳐진 물리량을 나타낸다 [32]. 또한, 계 사이의 상호작용에 의한 계의 변화를 서술한 과정 관계식은 변화의 의미를 강조하여 변화과정 관계식이라 명명할 것이며, 변화 의 원인을 명시하지 않은 “기술” 과 변화의 원인을 명시한

“설명” 을 구분하여 서술하고자 한다.

이러한 존재론적 범주구분을 바탕으로 본 연구에서는 Table 1과 같이 물리 관계식을 계 사이의 상호작용 관계만 을 서술하는 ‘상호작용관계식’ , 계 사이의 상호작용에 의한 계의 변화를 서술하는 ‘변화과정관계식’ 으로 구분하였다.

또한, 변화과정관계식은 계의 속성 변화만을 기술하는 ‘상 태관계식’ 과 계와 환경과의 상호작용에 의한 계의 속성들의 변화를 서술하는 ‘인과관계식’ 으로 구분하였다.

상호작용관계식은 질량, 거리, 전하 등과 같이 어떤 계 가 갖고 있는 속성 (property) 과 힘, 일 등과 같은 상호작 용 (interaction) 사이의 관계를 정량적으로 표현한 것으로 F = kqQ/r², F = GM m/r²등이 상호작용관계식에 해당 된다. F = kqQ/r²는 두 계가 갖는 전하량이라는 속성과 힘이라는 상호작용 사이의 관계에 대한 정량적 표현으로 두

Table 1. Classification of physics relationships (equations) within the framework of ontological categorization.

Category Descriptions of the Category Example

Interaction Relationship A representation of the quantitative relationship concerning certain • F = kqQ/r² interactions and relevant properties

Process State A representation of A representation of the quantitative relationship • x = x0+ vxt Relationship Relationship the change of certain concerning certain properties or a change of • P V = nRT

systems due to properties (describing only pattern without guessing interactions the origin of the pattern)

Causal A representation of the causal relationship between • F · t = ∆(mv) Relationship certain interactions among systems and environments • W = ∆Ek

and the change of properties of the system • F = kx (Explaining the origin of the change) • Q − W = ∆U

계가 갖는 전하량 사이의 상호작용 관계를 나타내고 있다.

F = GM m/r²도 역시 두 계가 갖는 질량이라는 속성과 힘이라는 상호작용 사이의 관계에 대한 정량적 표현으로 두 계가 갖는 질량 사이의 상호작용 관계를 나타내고 있다.

상태관계식은 계의 위치, 속도, 압력, 부피, 온도 등과 같 이 계가 갖고 있는 속성들의 정량적인 관계에 대한 표현으로 x = x₀+ v_xt, P V = nRT 등이 상태관계식에 해당된다.

x = x₀+ v_xt는 계가 갖는 위치와 속도라는 속성들의 정량 적인 관계에 대한 표현으로 위치 변화라는 계의 속성 변화를 나타낸다. P V = nRT 는 계가 갖는 압력, 부피, 온도라는 속성들 사이의 정량적인 관계에 대한 표현이다.

인과관계식은 질량, 속도, 운동량, 에너지, 압력, 부피 등의 속성과 힘, 일, 열 등의 계와 환경과의 상호작용에 대응하는 양들 (quantities) 을 포함하는 정량적 표현이다.

이를테면 충격량 운동량 정리, F · t = ∆(mv) 는 힘 (혹은 충격량) 이라는 상호작용이 원인으로 작용하여 운동량이라 는 계의 속성이 변화되는 결과를 보여주고 있다. W = ∆Ek

는 일이라는 상호작용이 원인으로 작용하여 운동에너지라 는 속성이 변화되는 결과를 보여주고 있다. 열역학 1법칙 Q− W = ∆U 는 열과 일이라는 상호작용이 원인으로 작용 하여 계의 내부에너지라는 속성이 변화됨을 보여준다.

위와 같이 물리학에서 사용하는 관계식을 존재론적 범 주의 차원에서 분류해보는 것은 타당한 근거를 가지며 교 육적으로도 의미가 있다고 판단된다. 왜냐하면 첫째, 물리 관계식이 갖고 있는 각각의 개념을 계, 속성, 상호작용이라 는 존재론적 범주로 구분하여 이해함으로써 개념에 대한 이해를 깊게 할 수 있다. 둘째, 물리 관계식을 상호작용관계 식, 상태관계식, 인과관계식으로 구분함으로써 각 관계식이 갖고 있는 기본적인 물리적 의미를 더욱 잘 이해할 수 있다.

그러므로 존재론적 범주 차원에서 물리식을 살펴보는 것은 물리식에 대한 수학적 설명과 이해에 익숙해 있는 학생들 에게는 더욱 필요한 과정일 수 있다.

3. 물리식의 물리적 의미 2: 인식론적 차원

Swann [33]은 학생들이 새로운 개념을 이해할 때 개념을 만든 과정과 같은 경로를 따라야 한다고 지적했다. 이는 학생들이 뉴턴과 아인슈타인과 똑같은 과정을 거치면서 학습을 해야 한다는 말이 아니라 새로운 개념이 만들어지는 인식적 과정에 맞게 개념을 학습해야 한다는 뜻이다. 즉, 실험 혹은 관측 결과에서 규칙성을 추출하여 구한 법칙을 학습하는 것이 목적이라면 학생들도 실험등을 통해 관련된 개념을 학습해야 한다. 또한 사고에 의해 구축된 의미라면 사고에 기반한 교수학습과정을 통해 새로운 의미를 받아들 여야 한다. 즉 실험에 의해 관측된 사실의 규칙성을 드러내 는 법칙은 실험적 확증에 의해 논의되고 학습되어야 하며, 실험결과의 기술을 넘어서는 원리는 이론적 논증에 의해 설명되고 학습되어야 한다. 이와 같이 교수학습 상황에서 물리지식을 다룰 때 지식이 전체 이론 안에서 갖는 역할에 맞게 다룰 필요가 있다. 특정한 물리식 (이를테면 뉴턴의 2 법칙) 이 전체 이론 (이를테면 뉴턴 역학) 에서 갖는 역할과 위상을 본 연구에서는 해당 식의 인식론적 차원의 의미라고 부르겠다.

하나의 식의 인식론적 의미는 다양하게 논의될 수 있다.

이를테면 역사적으로 뉴턴 2법칙의 인식론적 지위와 역할에 대한 여러 논의들이 있어왔다. 2법칙은 질량 m 인 물체에 가해진 힘은 속도의 변화 즉, 가속도를 유발한다는 ‘원리’

라는 의미를 가질 수 있다. 2법칙은 또한 어떤 질량이 갖는 가속도를 통해 가해진 힘을 알 수 있다는 의미에서 ‘힘의 정의’ 라는 의미를 가질 수 있다. 2법칙은 또한 어떤 힘을 가하여 속도의 변화를 측정함으로써 질량을 구할 수 있다는 점에서 ‘질량의 정의’ 를 의미하는 것으로도 이해할 수 있다 [34].

그런데 이러한 의미적인 복잡성을 뒤로 하고 단순히 힘을 질량과 가속도의 곱이라고 서술하는 것은 단지 이 식이 갖고

Table 2. Categorization of the epistemological meanings of physics equations.

Category Descriptions of the Category Example

Through Empirical Describing relation and regularity among observable variables • T = 2π√ l/g

Observation Law • dA/dt = k

• T²= kR³

• P V = nRT Through Definition Defining the meaning of a physics concept • v = s/t

Reasoning • p = mv

• K = mv²/2

• Ug = mgh

• I = q/t Principle Fundamental ideas (similar to axiom in mathematics) beyond • F = ma

the direct empirical verification • I = ∆P

• Q = ∆U + P ∆V

있는 구문론적인 (syntactic) 수학적 서술이라고 할 수 있다.

그런데 물리식 F = ma 는 뉴턴역학이라는 이론체계에서 원리나 정의라는 역할을 하고 있으므로 ‘힘은 질량과 가 속도의 곱이다.’ 라는 수학적 서술만으로 F = ma 가 갖고 있는 물리식의 의미를 모두 담아낼 수 없다.

현재 고등학교 물리 I 교과서들 [25,26]에서는 F = ma 가 실험결과로부터 추출 가능한 규칙성을 기술하는 것처럼 제시하고 있다. 예컨대, 용수철저울, 수레, 디지털 카메라 등을 이용한 실험을 통해 물체에 작용하는 힘 (접촉을 통 한 탄성력) 과 가속도의 관계가 비례하고, 물체의 질량과 가속도의 관계가 반비례한다는 실험 관찰 결과들로부터 F = ma를 입증된 것처럼 제시하고 있다. 그런데 F = ma 에서 힘은 알짜힘을 의미하며, 이것은 직접 측정되지 않는 개념이다. 따라서 측정되지 않는 개념을 포함하는 F = ma 는 원칙적으로 측정을 통해 직접 검증가능한 패턴이 아니고, 관측결과를 설명하는 과정에서 사용되는 이론적인 원리에 가깝다.

이와 같이 경험의 기술보다는 사고에 의해 만들어진 식을 교과서에서 실험을 통해 학습할 수 있는 것처럼 다룬다는 것은 짚고 넘어가야 할 문제이다. 사고에 의해 만들어진 새로운 이론을 실험을 통해서 학습할 때 다음과 같은 문 제들이 제기될 수 있기 때문이다. 첫째, 학생들이 정직한 관측을 경험할 수 있는 기회를 박탈할 수 있다. 왜냐하면 사고를 통해 만들어진 원리를 실험을 통해 도입하는 것은 사고의 비약이나 의도적 거짓 없이는 불가능하기 때문이다.

둘째, 이러한 학습 방법은 학생들로 하여금 모든 물리학에 관련된 이론들은 과학적 실증에 의한 방법에 의해 성립될 수 있다는 잘못된 과학의 본성을 심어 줄 수 있다. 즉 물리학의 법칙이나 이론들이 ‘다양한’ 과학적 방법에 의해 물리학 지식을 이룸에도 불구하고 모든 과학 관련 법칙이나 이론

들이 실험에 의해 만들어지고 증명될 수 있다고 생각하게 할 수 있는 것이다.

학생들이 새로운 개념을 학습할 때 개념을 만든 과정과 같은 경로를 따라야 한다는 Swann [33]의 입장을 받아들인 다면 물리식을 그것이 포함된 이론 안에서의 역할과 위상에 따라 구분하는 것이 교육적으로 의미 있을 것이다. 이를 테면 Spurgin은 물리식을 구성하는 2가지 요소가 “정의”

와 “법칙의 표현” 이라고 주장하였다 [35]. 한편 Halloun은 물리 개념의 인식론적 체계를 상위범주, 기본수준, 하위범 주라는 3 수준을 나누고 있으며 각각 이론, 모형, 개념으로 설명하고 있다 [30]. 여기서 기본 수준에 해당하는 모형은 하위 범주인 물리 개념과 상위 범주인 이론을 연결 시켜주는 인식론적 비계라고 할 수 있다.

물리학의 아이디어들을 전체 지식구조에서 갖는 역할과 위상에 따라 구분하는 것은 과학철학의 주요 논의거리이기 도 하였다. 이를테면 Campbell [36]은 법칙과 이론을 구분 하였고 이러한 구분은 오늘날 영향력있는 연구자들에 의해 과학의 본성의 주요 학습목표로 여겨지고 있다. Campbell 은 더 나아가서 과학이론의 구성요소들을 공리계, 경험적 결정 내용, 사전적 정의의 개입으로 구분하기도 하였다.

이후에 Carnap, Nagel, Harre, Toulmin, Giere 등이 과학 지식의 기능과 위상에 따른 구분에 대해서 다양한 논의를 제기하였고 이와 관련된 교육적 시사점도 논의된 바 있다 [37].

본 연구에서는 Table 2와 같이 물리식을 그것이 포함된 이론 안에서의 역할에 따라 정의, 경험법칙, 원리 등으로 구분하는 것을 제안하고자 한다. 모든 물리지식을 정의, 경험법칙, 원리라는 세 범주로 구분할 수 있는 것은 아니다.

그렇지만 정의, 경험법칙, 원리라는 세 범주를 구분하는 것이 교수학습을 위해 도움이 될 수 있다는 입장에서 이 세

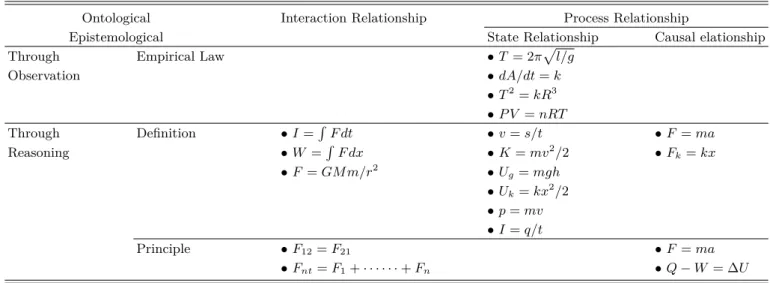
Table 3. Matrix of physics equations’ meanings based on the ‘ontological’ and ‘epistemological’ dimension.

Ontological Interaction Relationship Process Relationship

Epistemological State Relationship Causal elationship

Through Empirical Law • T = 2π√

l/g

Observation • dA/dt = k

• T²= kR³

• P V = nRT

Through Definition • I =∫

F dt • v = s/t • F = ma

Reasoning • W =∫

F dx • K = mv²/2 • Fk= kx

• F = GMm/r² • Ug= mgh

• Uk= kx²/2

• p = mv

• I = q/t

Principle • F12= F21 • F = ma

• Fnt= F1+· · · + Fn • Q − W = ∆U

범주를 구별하고자 한다. 세 범주 중에 경험법칙은 관찰에 의한 관계식에 속하고, 정의나 원리는 사고에 의한 관계식에 속하는 것으로 볼 수 있다.

경험법칙은 관찰 (측정) 사실의 규칙성이나 관찰 가능한 변인들 사이의 관계를 서술한 물리식으로 T = 2π√

l/g, dA/dt = k (케플러2법칙), T² = kR³ (케플러3법칙) 이 경험법칙의 사례가 된다. 정의는 물리 개념에 대한 의미를 규정하는 것으로 속도, 운동량, 운동에너지, 위치에너지, 전류 개념의 정의는 각각 v = s/t, p = mv, K = mv²/2, U_g = mgh, I = q/t 이라는 물리식과 관련된다. 윈리는 실험이나 측정을 통해 직접적인 증명이 불가능하며, 이론의 토대가 되는 아이디어로 수학에서 공리와 유사한 역할을 한다. 원리를 나타내는 물리식으로 F = ma, I = ∆mv, Q− W = ∆U 를 예로 들 수 있다¹.

경험법칙, 정의, 원리는 관찰과 사고라는 다른 근원을 갖기 때문에 교수학습에서 관찰에 의한 관계식을 사고에 의한 관계식과 구분하여 설명하고 학습하여야 한다. 이를 테면 앞서 논의한 바대로 F = ma 는 교수학습에서 정의와 원리로서의 의미를 갖는 것으로 다룰 수 있지만 이 식을 경험법칙처럼 취급하는 것은 피하는 것이 바람직하다.

3.2절과 3.3절에서 논의한 물리식이 갖는 존재론적 차 원과 인식론 차원의 의미를 종합하고 각 범주에 해당하는 대표적인 물리식을 정리한 결과가 [Table 3] 이다. 예컨대, P V = nRT라는 식은 존재론적 범주에서 살펴보면 계가 갖는 압력, 부피, 온도라는 속성들의 정량적인 관계에 대한

1물리학에서 법칙, 원리 등은 명확한 의미규정 없이 중첩된 의미를 가진 체로 사용되고 있다. 따라서 관습적으로 합의된 ‘원리’ 의 의미는 없 다고 보는 것이 정확할 것이다. 본 연구의 ‘원리’ 에 대한 규정은 뉴턴 제2법칙처럼 물리학 이론의 토대가 되는 핵심지식을 ‘원리’ 로 규정한 선행연구를 따른다 [37].

수학적 표현으로 계의 속성 변화만을 설명하고 있으므로 변화과정을 설명하는 관계식 중 상태방정식에 해당된다.

다른 한편으로 이 식은 인식론적 범주에서 살펴보면 압력, 부피, 온도라는 관찰 가능한 변인들 사이의 관계, 관찰 사 실의 규칙성을 나타내고 있으므로 경험법칙을 나타내는 관계식으로 분류될 수 있다.

Table 3에서 경험법칙을 나타내는 관계식은 모두 상태 관계식에 속하는 반면 원리를 나타내는 관계식은 상태 관 계식에 속하지 않는다는 것을 주목할 만하다. 즉 실험 관 찰을 통해 획득된 지식인 경험법칙을 나타내는 관계식은 관측가능한 속성들 사이의 관계만을 기술할 수 있다. 또한 사고에 의한 원리를 나타내는 관계식은 직접적 관측이 불 가능한 상호작용이나 인과 관계를 포함하므로 관측가능한 속성들의 관계를 기술하는 상태관계식일 수 없다. 또한, 정의를 나타내는 관계식은 존재론적 범주에서 상호작용, 상태, 인과 관계의 의미를 모두 가질 수 있음을 알 수 있다.

하나의 물리식이 반드시 표의 분류 중 하나의 영역에 배타적으로 속하는 것은 아니며, 하나의 식이더라도 맥락과 해석에 따라 다양하게 범주화 될 수 있다. 이를테면 앞서 논의한 바대로 F = ma 는 사고에 의한 관계식으로 정의를 나타내거나 원리를 나타내는 관계식으로 생각할 수 있다.

이것을 반영하여 표에서 F = ma 를 두 영역에 위치시켰다.

이와 같이 다양한 의미를 가질 수 있으며 복수로 범주화될 수 있는 식은 교수학습에서 특별한 주의를 기울일 필요가 있다.

학생들은 물리식이 가질 수 있는 존재론적, 인식론적 의 미와 관련하여 개념적인 어려움을 가질 수 있다. 이를테면 학생들은 인과관계식에 속하는 물리식을 상호작용 관계식인 것으로 혼동할 수 있으며, 원리에 속하는 물리식을 경험법 칙에 속하는 물리식으로 잘못 판단할 수 있다. 이와 관련된

본 연구자들의 연구 결과는 별도의 논문으로 발표하고자 한다.

IV. 결론 및 제언

본 연구는 문제풀이를 위한 도구를 넘어서 물리식이 갖는 다양한 의미를 체계화한 연구이다. 이를 위해 본 연구는 물리식의 의미에 대하여 세 수준의 위계성을 갖는 분석을 수행하였다. 먼저 수학식과 구분되는 물리식의 특징을 분 석하여 물리식이 갖는 수학식과의 차이점을 알아보았다.

다음으로 물리식에 대한 물리적 서술과 수학적 서술이 갖는 의미와 차이점을 분석하여 물리식에 대한 물리적 서술의 중요성을 알아보았다. 마지막으로 물리식이 갖는 물리적 의미를 존재론적 범주 차원과 인식론적 차원에서 논의하 였다.

본 연구는 다음과 같은 교육적 시사점을 갖는다. 첫째, 본 연구와 같은 물리식의 범주화는 학생들로 하여금 물리식에 대한 이해의 폭을 다양하게 할 수 있는 교수학습을 위한 토 대를 제공할 수 있다. 특히 본 연구에서 제안하는 존재론적 범주와 인식론적 범주를 종합하는 틀과 Table 3과 같은 인 식론적 , 존재론적 의미의 종합은 물리 교수학습의 설계에서 도움이 될 수 있다. 이를테면 앞선 논의에서 F = ma 는 정의를 나타내거나 원리를 나타내는 관계식이므로 사고에 의한 관계식에 속한다. 이러한 관계식을 일종의 경험법칙을 나타내는 관계식으로 다루는 현재의 관행은 개념의 이해와 관련하여 여러 가지 문제를 일으킬 수 있다.

둘째 본 연구에서 다루었던 물리식이 갖는 여러 차원의 의 미를 교수학습에서 다룸으로써 물리식에 대한 학습자의 이 해를 높일 수 있을 것이다. 학습자의 물리식에 대한 이해의 수준을 단지 공식에 수를 대입해서 문제를 해결하는 기초적 수준에서 역사적, 철학적 맥락까지 고려된 개념적 수준으로 높일 수 있을 것이며, 물리식에 대한 이해를 통하여 물리 개념, 법칙, 원리의 이해를 증진할 수도 있을 것이다. 또한, 물리식과 수학식이 갖는 차이점을 이해하고, 물리식의 수 학적 서술과 물리적 서술의 차이를 이해함으로써 물리식이 갖고 있는 다양한 의미를 깊이 있게 이해할 수 있을 것이다.

셋째, 과학과 기술의 역사적 발전과정에서 수학의 기여는 당연히 인정받아야 하지만 과학자의 양성이 아닌 과학적 소양을 목표로 하는 과학교육 특히, 오늘날의 물리 교육에 서 수학의 지나친 강조는 재고할 여지가 있다. 특히, 물리 교육에서 수학의 모습이 가장 잘 드러나는 물리식에 관한 교육의 모습에서는 더욱이 그러하다. 물리식에 대한 물리적 의미에 대한 논의보다는 식이 갖고 있는 수학적 의미와 이 를 활용한 문제풀이에 집중하는 것이 현실의 한 측면이다.

이러한 문제를 해결하기 위하여 학생들이 물리식에 관한 수학적 서술보다는 물리적 서술을 통하여 물리식이 갖고 있는 물리적 의미에 대하여 학습 할 수 있게 해야 한다. 물 리식이 이론 안에서 갖는 역할이나 각 물리식이 갖고 있는 개념들 사이의 관계를 알아보는 것은 학생들로 하여금 식이 갖는 물리적 의미를 이해할 수 있게 하고, 물리적 개념뿐만 아니라 과학이 갖고 있는 본성에 대한 이해에도 도움이 될 것이다.

넷째, 주요한 몇가지 물리식에 대해 물리 교재에서 제시되 는 서술들을 검토하면 전반적으로 식의 존재론적, 인식론적 의미에 대한 서술이 부족하다는 것을 어렵지 않게 확인할 수 있다. 식들은 발견과 정당화의 맥락없이 받아들여야 할 중요한 식으로 급작스럽게 제시되기도 하며, 인식론적 존재론적 차원의 의미에 대한 서술을 찾아보기 힘든 경우도 많다. 대신에 교재에 제시되는 물리식에 대한 서술은 물리 식의 문법적 구조 해석에 충실한 수학적 서술에 가깝기도 한데, 교재의 이러한 문제점에 대한 주의가 필요하다.

REFERENCES

[1] R. D. Knight, Five Easy Lesson (Addison Wesley, San Francisco, 2004), p. 26.

[2] Y. Gingras, History of Science 39, 3 (2001).

[3] E. Zahar, The British Journal 31, 3 (1980).

[4] O. Uhden, R. Karam, M. Pietrocola and G. Pos- piech, Sci. Educ. 21, 489 (2012).

[5] H. Kragh, Sci. Educ. 24, 516 (2015).

[6] T. H. Kjeldsen and J. Lutzen, Sci. Educ. 24, 555 (2015).

[7] Y. Gingras, Sci. Educ. 24, 529 (2015).

[8] B. L. Sherin, Cognition and Instruction 19, 479 (2001).

[9] A. B. Arons, Teaching Introductory Physics (John Wiley & Sons, Inc., New York, 1997), p. 99.

[10] D. Hestenes, Am. J. Phys. 55, 440 (1987).

[11] J. Y. Na and J. W. Song, The Korean Society of Elementary Science Education 29, 300 (2010).

[12] S. G. Bruch, Sci. Educ. 24, 495 (2015).

[13] R. L. Gay, J. M. Saez and J. M. Torregrosa, Sci.

Educ. 24, 591 (2015).

[14] F. B. Kneubil and M. R. Robilotta, Sci. Educ. 24, 645 (2015).

[15] E. F. Redish and E. Kuo, Sci. Educ. 24, 561 (2015).

[16] R. Karam and O. Krey, Sci. Educ. 24, 661 (2015).

[17] G. Lloyd and N. Sivin, The Way and The Word (Yale University Press, New Haven and London, 2002), p.

167.

[18] R. Dugas, A History of Mechanics (Dover Publica- tions, Inc., New York, 1988), p. 33.

[19] Y. S. Kim and K. S. Im, The Introduction of Scien- tific History (Dasan, Seoul, 2007), p. 161.

[20] http://plato.stanford.edu/archives/ (accessed Mar., 11, 2014).

[21] L. Hansson, O. Hansson, K. Juter and A. Redfors, Sci. Educ. 24, 615 (2015).

[22] P. G. Hewitt, The Physics Teacher 49, 264 (2011).

[23] M. J. Moelter and M. Jackson, The Physics Teacher 50, 472 (2012).

[24] J. Walker, Halliday & Resnick Fundamentals of Physics (John Wiley & Sons, Inc., Jefferson City, 2011), p. 91.

[25] Y. M. Kim, I. K. Kim, S. W. Kim, B. Y. Park and B.

H. Cheong et al., High School Physics I (Gyouhaksa, Seoul, 2011), Chap. 1.

[26] S. I. Kwak, S. H. Ryou, D, G. Kim, J. J. An and O. S.

Lee et al., High School Physics I (Chunjaegyoyouk, Seoul, 2011), Chap. 1.

[27] R. A. Serway and C. Vuille, College Physics (Brooks/Cole, Boston, 2012), p. 539.

[28] H. D. Young and R. A. Freedman, University Physics (Addison-Wesley, San Francisco, 2012), p.

734.

[29] M. T. H. Chi, J. D. Slotta and N. Leeuw, Learning and Instruction 4, 27 (1994).

[30] I. A. Halloun, Modeling Theory in Science Education (Springer, Dordrecht, The Netherlands, 2006), p. 51.

[31] E. Etkina, A. Warren and M. Gentile, The Physics Teacher 44, 35 (2006).

[32] Y. W. Cheong and J. W. Song, New Phys.: Sae Mulli 61, 850 (2011).

[33] W. F. G. Swann, Am. J. Phys. 19, 182 (1951).

[34] R. S. Westfall, The Construction of Modern Sci- ence (The Cambridge University Press, Cambridge, 1971), p. 152.

[35] C. B. Spurgin, Physics Education 19, 114 (1984).

[36] N. R. Campbell, Physics: The Elements (Cambridge University Press, Cambridge, 1920), p. 113.

[37] Y. W. Cheong, Journal of the Korean Association for Science Education 34, 459 (2014).