A New Robust Output Feedback Variable Structure Controller for Uncertain More Affine Nonlinear Systems with Mismatched Uncertainties and Matched Disturbance
전체 글
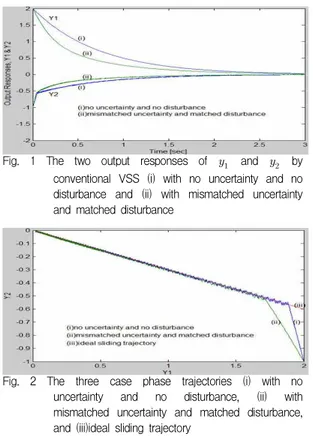
수치
관련 문서
MR: Start and end mode output selection, shown here as 0 (output an END output signal on a high or low limit error so that the next weld cycle can start)a. The other selection is
in Mealy machines, input change can cause output change as soon as logic is done – a big problem when two machines are interconnected – asynchronous feedback may occur if
Nonlinear Optics Lab...
In this paper, we proposed a novel interactive medical image retrieval framework with relevance feedback based on pairwise constraint propagation, which takes
In this paper, we investigate a long-time behavior of global solutions to the initial boundary problem of nonlinear dispersive-dissipative wave equation with time-dependent
In utilizing negative feedback to improve the properties of an amplifier under design, the starting point in the design is the selection of the feedback topology appropriate
is unilateral and that the forward transmission through the feedback is negligibly small. - The actual input and output R of the
Figure 8.4 The four basic feedback topologies: (a) voltage-mixing voltage-sampling (series–shunt) topology;.. (b) current-mixing current-sampling (shunt–series)