Application of quasi-Monte Carlo methods in multi-asset option pricing

(1)

2013, 24

(

4)

,

669–677

준난수 몬테칼로 방법을 이용한 다중자산 옵션 가격의 추정

모은비

¹

· 박종선

²

12성균관대학교 통계학과

접수 2013년 5월 3일, 수정 2013년 5월 24일, 게재확정 2013년 5월 29일

요 약

본 연구에서는 다중자산 옵션 가격의 추정에 있어 자산의 수, 상관계수, 자산의 값들과 표준편차의 여러 조합에 대한 시뮬레이션을 통하여 저불일치 수열에 따르는 준난수 몬테칼로 방법들을 비교하였 다. 결과적으로 준난수와 모로 역변환을 이용하는 것이 기본적인 몬테칼로 방법보다 정확하였으며 자 산의 수와 관계없이 준난수 방법들 중 혼합법들이 더욱 효과적임을 알 수 있었다.

주요용어: 다중자산옵션, 모로 역변환, 준난수, 준몬테칼로.

1. 서론

의사난수 (pseudo-random number)를 이용하여 적분 등의 문제를 해결하는 몬테칼로 방법은 수식적 으로 해를 구할 수 없는경우나 차원이 높아 수치적인 방법을 적용하는 것이 용이하지 않을 때 매우 유 용한 방법이다. 그러나 상대적으로 많은 시행 횟수가 필요하다는 단점을 보완하기 위해서 저불일치 수 열 (low discrepancy sequence)인 준난수 (quasi random number)를 사용할 수 있는데 준난수는 의사 난수보다 표본수가 적더라도 높은 균일성을 지니며 수렴속도가 빠르고 정확도도 향상 되는 것으로 알려 져 있다.

준 난수의 종류에는 Halton 수열 (Halton, 1964), Faure 수열 (Faure, 1982), Sobol 수열 (Sobol, 1967), 임의의 Sobol로 알려진 Owen 혼합법 (Owen, 1995), Faure-Tezuka 혼합법 (Faure와 Tezuka, 2002), Owen-Faure-Tezuka 혼합법 (Hong과 Hickernell, 2003)이 있다. 본 연구에서는 여러 가지 준난 수 방법들에 따라 만기에 권리행사가 가능한 유러피안 다중자산 옵션 (multi-asset option) 가격의 추정 에 대한 비교를 위하여 자산의 수와 가격, 그리고 표준편차의 여러 조합에 대하여 시뮬레이션을 실시하 고 그 결과들을 살펴보았다.

본 논문의 구성은 다음과 같다. 2절에서는 준몬테칼로 방법에 사용되는 준난수들과 정규난수의 추출 방법인 모로 역변환 (Moro, 1995)에 대하여 살펴보고, 3절에 다중자산 옵션에 대한 내용을 포함하였다.

4절에서는 몬테칼로 방법과 준몬테칼로 방법을 이용한 모의실험을 통해 다중자산 옵션의 가격을 추정하 고 이들의 결과를 비교하였으며 5절에서 논문의 결론과 향후 연구방향 등에 대하여 정리하였다.

1

(110-745) 서울시 종로구 성균관로 25-2, 성균관대학교 통계학과, 대학원생.

2

교신저자: (110-745) 서울시 종로구 성균관로 25-2, 성균관대학교 통계학과, 교수.

E-mail: cspark@skku.edu

(2)

2. 준난수 몬테칼로 방법과 모로 역변환

본 연구에서는 여러 저불일치 수열들 중 Halton 수열, Faure 수열, Sobol 수열, 그리고 임의의 Sobol로 알려진 Owen 혼합법, Faure-Tezuka 혼합법, 마지막으로 Owen-Faure-Tezuka 혼합법을 고려 하였다. 또한 가격의 추정에 있어 정도를 높여 각 방법의 비교에 정확성을 기하기 위하여 정규분포를 따 르는 난수의 추출에는 모로 역변환을 이용하였다. 저불일치 수열들과 모로 역변환에 대한 수식은 매우 복잡하며 논문의 주요 내용을 이해하는데 꼭 필요하지 않은 것으로 판단되어 생략하였으며 특징과 개괄 적인 부분만을 언급하였다.

2.1. 준난수 몬테칼로 방법

Halton 수열은 다차원 수열을 발생시키는 가장 단순한 방법이다. 보통 일차원 Halton 수열은 기저 (base) 2인 수열을 사용한다. Halton 수열은 각 차원이 서로 다른 기저를 가지며, 이때 사용 되는 기저 는 소수이다. 1차원 일 때는 첫 번째 소수인 2를 기저로 사용하고, 2차원일 때는 첫 번째, 두 번째 소수 인 2와 3을 기저로 사용한다. Halton 수열의 경우에는 차원이 6 또는 8 이상인 경우 상관관계가 커지는 문제가 있는 것으로 알려져 있다.

Halton 수열이 각 차원 마다 다른 소수를 사용하는데 반해 Faure 수열은 하나의 소수를 사용하게 되 는데, 전체 차원 보다 크거나 같은 소수 중에 가장 작은 소수를 사용한다. 즉, Halton 수열은 s차원을 나타낼때는 s개의 소수를 필요로 하지만 Faure 수열은 하나의 소수로 나타낼 수 있다. 예를 들어, 4차 원일 경우 Halton 수열에서는 각 차원에 2, 3, 5, 7의 소수를 기저로 사용하여 난수를 구하나 Faure 수 열은 1, 2, 3, 4차원의 모든 난수를 4보다 크거나 같은 소수 중에 가장 작은 소수인 5를 기저로 사용하여 구한다. Faure 수열도 Halton 수열과 비슷하게 높은 차원에서의 상관관계 문제를 가지고 있다.

1967년 Sobol에 의해 소개된 Sobol 수열은 준몬테칼로 방법 중에 가장 많이 사용되는 방법으로 주어 진 초기값의 원시다항식 (primitive polynomial)을 사용하여 각 차원에 해당하는 난수를 구하는 방법이 다. Sobol 수열의 난수를 구하기 위해서는 XOR 연산이 필요하며 차원이 증가할수록 시간이 오래 걸린 다는 단점이 있다. 이를 해결하기 위해 Antonov와 Saleev (1979)는 Gray Code를 이용하여 Sobol 수 열을 구하였고, 이 코드를 사용해도 각 수열의 간격은 변하지 않음을 증명하였다. Sobol 수열은 균일 성이 좋고 계산시간이 적게 요구된다는 장점이 있으며, Galanti와 Jung (1997)은 260 차원까지 저하 현상이 없음을보였다. 기존 방법으로는 최대 40차원의 Sobol 수열을 생성할 수 있었지만, Joe와 Kuo (2003)는 최대 차원을 1111까지 확장 시켰다. 그러나 차원이 증가함에 따라 초기값의 상관도가 커지고, 각 차원간의 최대 상관계수 값이 매우 높아져서 균일성이 깨지는 결과가 나타나 수치적분 값의 오차가 증가하는 현상을 보였다.

기존의 준난수 수열은 Van der corput 수열과 관계가 있으나, 임의 준난수 수열은 디지털 수열과 관련이 있으며 임의 준난수 Sobol 수열로는 혼합 방법에 따라 Owen 혼합법, Faure-Tezuka 혼합법, Owen-Faure-Tezuka 혼합법이 있다. 세 가지 혼합법은 기저를 소수로 사용하며 Sobol 준난수와 일반적 인 난수의 조합으로 생성된다. Owen 혼합법은 디지털 수열을 변형한 형태이며, Faure-Tezuka 혼합법 은 이를 재배치 한 뒤 필요한 디지털 수열을 얻고, Owen-Faure-Tezuka 혼합법은 Owen 방법과 Faure- Tezuka 방법을 혼합한 형태를 갖는다.

2.2. 모로 역변환

일반적으로 균일난수를 이용하여 표준정규분포로 변환 할 때 박스 뮐러 방법이 널리 이용되고 있다.

그러나이방법은 준 몬테칼로의 군집성을 줄이려는 특성을 파괴할 수 있어 적합하지 않은 것으로 알려

(3)

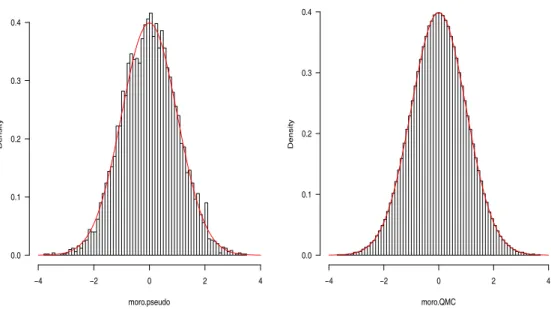
져 있다. 이의 해결을 위한 모로 역변환은 두 단계로 구성되어 있다. 1단계에서는 정규분포의 중앙부분 에 대한 난수를 구하는 부분으로 Beasley와 Springer (1977)가 제시한 알고리즘을 사용한다. 두 번째 단계에서는 나머지 정규분포의 양끝 꼬리부분에 대한 난수를 추출하게 된다. 일반적인 의사난수와 모로 방법을 이용하여 얻어진 정규난수의 결과는 Figure 2.1과 같다.

moro.pseudo

Density

−4 −2 0 2 4

0.0 0.1 0.2 0.3 0.4

moro.QMC

Density

−4 −2 0 2 4

0.0 0.1 0.2 0.3 0.4

Figure 2.1 Standard pseudo random numbers (left) and random numbers from Moro inversion (right)

3. 다중자산 옵션

옵션이란 상품이나 유가증권 등의 기초자산을 미리 정해진 가격 (행사가격)으로 지정된 날짜 (만기 일) 또는 그 이전에 사거나 팔 수 있는 권리로서 매수자가 자신에게 유리하면 권리를 행사하고 그렇지 않으면 권리를 포기할 수 있는 선택권을 말한다. 옵션에는 기초자산을 매수할 수 있는 권리인 콜옵션 과 매도할 수 있는 풋옵션이 있다. 다중자산 옵션은 기초자산이 여러 개인 경우이며 Stulz (1982)와 Johnson (1981)은 자산이 두 개일 경우에 이론가격을 구하는 식을 제시하였다. Johnson (1987)은 블 랙-숄즈 방정식에 관한 직관적인 접근과 Cox와 Ross (1976)의 접근법, Margrabe (1978)가 사용한 기 법에 기반하여, 다중자산으로 확장시키는 경우를 표현하였다. Wu와 Zhang (1999)은 자산이 두 개인 경우, 분산감소기법 및 산술평균, 기하평균을 이용하여 옵션 가격을 추정하였다. Levy (2004)는 자산 이 3개일 경우 준몬테칼로 방법과 몬테칼로 방법을 이용하여 수치적 해를 구하여 비교하였고, Boyle 등 (1989)는 CRR 모형을 이용하여 수치적 해를 구하였다. 다중자산 옵션들 중 최대값을 갖는 자산과 최소 값을 갖는 자산에 대한 이론적인 가격 (Cmax, Cmin)은 다음과 같다.

(4)

[ 표기법 ]

S

i

: i 번째 기초자산의 초기 가격 , i = 1, · · · , I

K: 행사가격

r: 무위험 이자율 ( 모든 자산에 대하여 동일 ) T : 만기시점

σ

_i

: i 번째 기초자산의 변동성 ( 표준편차 ), i = 1, · · · , I

ρ

ij

: i 자산과 j 자산 사이의 상관계수 , i ̸= j, i = 1, · · · , I, j = 1, · · · , I

Cmax = S1NI(d1(S1, K, σ₁²), d^∗₁(S1, S2, σ₁₂² ), · · · , d^∗₁(S1, SI, σ_1I² ), ρ112, ρ113, · · · ) + S2NI(d1(S2, K, σ2²), d^∗1(S2, S1, σ21² ), · · · , d^∗1(S2, SI−1, σ2(I−1)² ), ρ112, ρ113, · · · )

+ · · · (3.1)

+ SINI(d1(SI, K, σ²_I), d^∗₁(SI, S1, σ²_I1), · · · , d^∗₁(SI, SI−1, σ²_(I−1)I), ρ112, ρ113, · · · )

− Ke^−rT(1 − NI(−d2(S1, K, σ²₁), −d2(S2, K, σ₂²), · · · , −d2(SI, K, σ²_I), ρ12, ρ13, · · · )) Cmin = S1NI(d1(S1, K, σ₁²), −d^∗₁(S1, S2, σ²₁₂), · · · , −d^∗₁(S1, SI, σ²_1I), −ρ112, −ρ113, · · · )

+ S2NI(d1(S2, K, σ2²), −d^∗1(S2, S1, σ²21), · · · , −d^∗1(S2, SI−1, σ²2(I−1)), −ρ112, −ρ113, · · · )

+ · · · (3.2)

+ SINI(d1(SI, K, σ²_I), −d^∗₁(SI, S1, σ_I1² ), · · · , −d^∗₁(SI, SI−1, σ_(I−1)I² ), −ρ112, −ρ113, · · · )

− Ke^−rTNI(d2(S1, K, σ²₁), d2(S2, K, σ²₂), · · · , d2(SI, K, σ_I²), ρ12, ρ13, · · · )

여기서, d^∗1(Si, Sj, σ_ij²) = ln(^Si/S_j)^+0.5σ²ijT σ_ij√

T , d1 = ln(S_i/K)+(r+0.5σ²_i)T σ_i√

T , d2 = d1− σi

√T , σ_ij² = σ_i²−

2ρijσiσj+ σ²_j, ρiij = ^σⁱ^−ρ_σ^ij^σ^j

ij , ρijk = ^σⁱ²^−ρ^ij^σⁱ^σ^j^−ρ_σ^ik^σⁱ^σ^k^+ρ^jk^σ^j^σ^k

ijσ_ik , i = 1, · · · , I, j = 1, · · · , I, k = 1, · · · , K이며 NI()는 I차원 다변량 정규분포이다.

예를 들어 자산이 세 개 (I = 3)인 경우 기초자산 가격 (S1, S2, S3)과 행사가격 (K)이 모두 100으 로 같고 (S1 = S2 = S3 = K = 100), 무위험 이자율 r이 0.04, T = 1, 변동성 σi = 0.2 (∀i = 1, · · · , I)이며 상관계수 ρij= 0.5 (∀i ̸= j, i = 1, · · · , I, j = 1, · · · , I)일 때, 이론적인 최대값과 최소 값은 18.0272와 3.2972가 된다.

4. 모의실험 및 결과

이 절에서는기본적인 몬테칼로 방법과 준몬테칼로 방법들이 다중자산 옵션 가격의 추정에 미치는 영 향을 알아보고 정확성을 비교하기 위한 모의시험 결과를 정리하였다.

우선 옵션의 행사가격 (K = 100), 무위험 이자율 (r = 0.04), 잔존 만기시점 (T = 1) 값들은 변동을 주지 않고 고정된 하나의 값들을 사용하였다. 그 이외에 자산의 표준편차 (σi)는 모든 자산에 대하여 동 일한값으로 0.2와 0.9를 고려하였고 자산들 사이의 상관계수로는 0.5와 0.9를 사용하였다. 0.5는 다중 자산옵션에 대한 시뮬레이션에서 주로 사용되는 값이며 0.9는 일반적인 범위를 벗어나는 높은 값을 갖 는경우 방법들의 차이를 살펴보기 위하여 사용하였다. 자산의 수는 3∼6개인 경우를 고려하였는데 자 산의가격이 80과 100으로 모두 같은 경우와 모두 다른 경우를 고려하였다. 자산의 가격이 다른 경우에 는 순서대로각각 80, 100, 120, 140, 160, 180을 초기 가격으로 사용하였다. 예를 들어 자산의 4개인 경 우에는 순서대로 S1= 80, S2= 100, S3 = 120, S4= 140을 사용하였다. 반복회수 (N )는 여러 값에 대 한 시도를 통하여 시뮬레이션 추정치가 수렴하는데 충분한 100,000으로 고정하여 추정치의 정확성을 비 교하는데 초점을 두었다. 다중자산 옵션의 가격과 이의 표준오차를 추정하기 위한 모의실험 알고리즘이 Figure 4.1에 정리되어 있다.

(5)

[Step 1] Initialize S

_i

, K, r

_i

, T , σ

_i

, ρ

_ij

, N : N is the number of repetition.

∀i ̸= j, i = 1, · · · , I, j = 1, · · · , I

Repeat Step 2, Step 3-1, and Step 3-2 N times (n = 1, · · · , N ).

[Step 2] Generate Z ∼ N

I

(µ, Σ) with µ, Σ

µ = T ×







r

₁

− σ

²₁

/2 r

₂

− σ

²₂

/2

. . . r

_I

− σ

_I²

/2





 , Σ =







σ

²₁

σ

₁

σ

₂

ρ

₁₂

· · · σ

₁

σ

_I

ρ

_1I

σ

₂

σ

₁

ρ

₂₁

σ

²₂

· · · σ

₂

σ

_I

ρ

_2I

. . .

. . . . . .

. . . σ

_I

σ

₁

ρ

_I1

σ

_I

σ

₂

ρ

_I2

· · · σ

²_I





 .

[Step 3-1] Let S

_i^T

= S

_i

e

^Z[i]

. Z[i] is the ith column of Z, i = 1, · · · , I.

[Step 3-2] For each n,

1) Maximum for call option: C

_maxⁿ

= max(max(S

₁^T

, S

^T₂

, · · · , S

_I^T

) − K, 0) 2) Minimum for call option: C

ⁿ_min

= max(min(S

₁^T

, S

^T₂

, · · · , S

^T_I

) − K, 0) [Step 4]

1) Maximum for call option: C ¯

max

=

_N¹

Σ

^N_n=1

C

_maxⁿ

2) Minimum for call option: C ¯

_min

=

_N¹

Σ

^N_n=1

C

_minⁿ

[Step 5-1] Estimate option price from ¯ C

_max

, ¯ C

_min

in Step 4.

1) Maximum for call option: C ˜

max

= e

^−rT

C ¯

max

2) Minimum for call option: C ˜

_min

= e

^−rT

C ¯

_min

[Step 5-2] Calculate standard error for option prices.

1) Maximum for call option: SE( ˜ C

_max

) = q

e−2rT

N −1

Σ

^N_n=1

(C

_maxⁿ

− ¯ C

_max

)

²

/ √ N 2) Minimum for call option: SE( ˜ C

_min

) =

q

e−2rT

N −1

Σ

^N_n=1

(C

_minⁿ

− ¯ C

_min

)

²

/ √ N

Figure 4.1 Simulation algorithm for multi-asset option

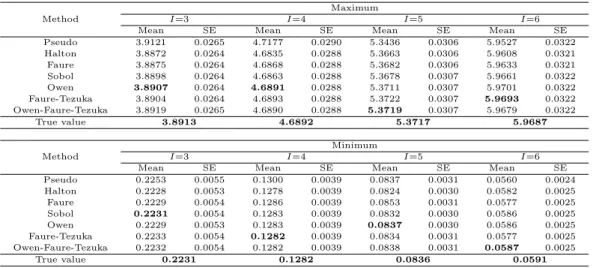
시뮬레이션 결과들 중 자산의 표준편차가 0.2인 경우와 자산의 가격이 동일한 경우에서는 가격이 모 두 80인 경우에 대한 결과들만 포함하였다. Table 4.1과 Table 4.2에는 자산의 가격이 80으로 모두 같 은경우 각 방법들에 따른 옵션가격의 추정치와 표준오차들이 포함되었고 각각의 자산 수에서 이론가격 과의 차이가 가장 작은 경우는 굵게 표시하였다.

Table 4.1 Mean and standard error estimates of maximum and minimum for σ

i

= 0.2, S

i

= 80, ρ

ij

= 0.5 (∀i, j)

Maximum

Method I=3 I=4 I=5 I=6

Mean SE Mean SE Mean SE Mean SE

Pseudo 3.9121 0.0265 4.7177 0.0290 5.3436 0.0306 5.9527 0.0322

Halton 3.8872 0.0264 4.6835 0.0288 5.3663 0.0306 5.9608 0.0321

Faure 3.8875 0.0264 4.6868 0.0288 5.3682 0.0306 5.9633 0.0321

Sobol 3.8898 0.0264 4.6863 0.0288 5.3678 0.0307 5.9661 0.0322

Owen 3.8907 0.0264 4.6891 0.0288 5.3711 0.0307 5.9701 0.0322

Faure-Tezuka 3.8904 0.0264 4.6893 0.0288 5.3722 0.0307 5.9693 0.0322 Owen-Faure-Tezuka 3.8919 0.0265 4.6890 0.0288 5.3719 0.0307 5.9679 0.0322

True value 3.8913 4.6892 5.3717 5.9687

Minimum

Pseudo 0.2253 0.0055 0.1300 0.0039 0.0837 0.0031 0.0560 0.0024

Halton 0.2228 0.0053 0.1278 0.0039 0.0824 0.0030 0.0582 0.0025

Faure 0.2229 0.0054 0.1286 0.0039 0.0853 0.0031 0.0577 0.0025

Sobol 0.2231 0.0054 0.1283 0.0039 0.0832 0.0030 0.0586 0.0025

Owen 0.2229 0.0053 0.1283 0.0039 0.0837 0.0030 0.0586 0.0025

True value 0.2231 0.1282 0.0836 0.0591

우선 상관계수가 0.5인 경우의 결과 (Table 4.1)를 살펴보면 자산의 수가 3개이며 최소값의 경우 Sobol 방법의 추정치가 가장 정확한 경우를 제외하고 모든 경우에서 혼합법들의 추정치와 이론가격과 의 차이가 가장 작았다. 혼합법들 간에는 자산의 수 등에 따른 특별한 추세는 없었으며 세 가지 방법들 중하나의 추정치가 가장 정확하였다.

(6)

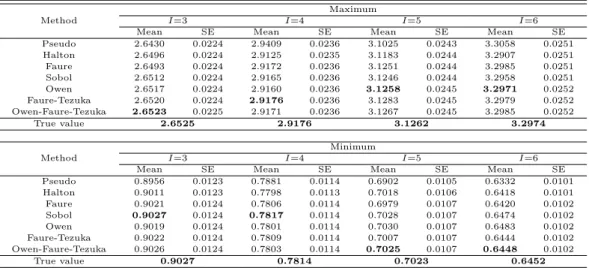
Table 4.2 Mean and standard error estimates of maximum and minimum for σ

_i

= 0.2, S

_i

= 80, ρ

_ij

= 0.9 (∀i, j)

Maximum

Pseudo 2.6430 0.0224 2.9409 0.0236 3.1025 0.0243 3.3058 0.0251

Halton 2.6496 0.0224 2.9125 0.0235 3.1183 0.0244 3.2907 0.0251

Faure 2.6493 0.0224 2.9172 0.0236 3.1251 0.0244 3.2985 0.0251

Sobol 2.6512 0.0224 2.9165 0.0236 3.1246 0.0244 3.2958 0.0251

Owen 2.6517 0.0224 2.9160 0.0236 3.1258 0.0245 3.2971 0.0252

True value 2.6525 2.9176 3.1262 3.2974

Minimum

Pseudo 0.8956 0.0123 0.7881 0.0114 0.6902 0.0105 0.6332 0.0101

Halton 0.9011 0.0123 0.7798 0.0113 0.7018 0.0106 0.6418 0.0101

Faure 0.9021 0.0124 0.7806 0.0114 0.6979 0.0107 0.6420 0.0102

Sobol 0.9027 0.0124 0.7817 0.0114 0.7028 0.0107 0.6474 0.0102

Owen 0.9019 0.0124 0.7801 0.0114 0.7030 0.0107 0.6483 0.0102

True value 0.9027 0.7814 0.7023 0.6452

상관계수가 0.9인 경우 (Table 4.2)에도 최소값의 경우에는 자산의 수가 3개와 4개인 경우 Sobol 방 법이 가장 정확한 결과를 나타내었으나 나머지의 경우에는 세 가지 혼합법들 중 하나가 가장 좋은 결과 를 나타내었다. 상관계수가 크거나 결과에는 포함하지 않았으나 표준편차가 큰 경우에는 자주 혼합법 이외의 방법들이 가장 정확한 것으로 나타나 혼합법들의 효율성이 떨어지는 것으로 판단된다. 추정치나 표준오차에서도 세 방법에 큰 차이는 보이지 않았다. Halton 수열을 이용하는 경우 자산의 수가 많아지 면 난수들 사이의 상관관계가 높아져 추정치의 오차가 커지는 현상을 보였다.

Table 4.3과 Table 4.4에는 표준편차가 0.2이고 상관계수는 앞에서와 같이 0.5와 0.9인 경우이면서 자산의기초가격이 모두 다른 경우에 대한 시뮬레이션 결과들이 포함되었다. 자산의 수도 앞에서와 같 이 3개에서 6개까지의 경우를 고려하였다.

Table 4.3 Mean and standard error estimates of maximum and minimum for σ

_i

= 0.2, S

₁

= 80, S

₂

= 100, S

3

= 120, S

4

= 140, S

5

= 160, S

6

= 180, ρ

ij

= 0.5 (∀i, j)

Maximum

Pseudo 26.9739 0.0695 47.5925 0.0857 68.8435 0.0982 90.7257 0.1103 Halton 27.0871 0.0698 47.5229 0.0854 68.9061 0.0979 90.5784 0.1098 Faure 27.0880 0.0698 47.5229 0.0854 68.9175 0.0979 90.5961 0.1099 Sobol 27.0926 0.0698 47.5232 0.0854 68.9176 0.0979 90.5988 0.1099 Owen 27.0926 0.0698 47.5264 0.0854 68.9206 0.0979 90.6055 0.1099 Faure-Tezuka 27.0925 0.0698 47.5277 0.0854 68.9245 0.0980 90.6055 0.1099 Owen-Faure-Tezuka 27.0934 0.0698 47.5259 0.0854 68.9222 0.0979 90.6032 0.1099

True value 27.0935 47.5267 68.9227 90.6055

Minimum

Pseudo 1.2471 0.0143 1.2233 0.0141 1.2298 0.0142 1.2316 0.0142

Halton 1.2236 0.0142 1.2217 0.0141 1.2201 0.0141 1.2197 0.0141

Faure 1.2236 0.0142 1.2217 0.0141 1.2210 0.0141 1.2208 0.0141

Sobol 1.2246 0.0142 1.2218 0.0142 1.2218 0.0141 1.2215 0.0141

Owen 1.2245 0.0142 1.2221 0.0141 1.2221 0.0141 1.2222 0.0141

True value 1.2248 1.2220 1.2219 1,2218

(7)

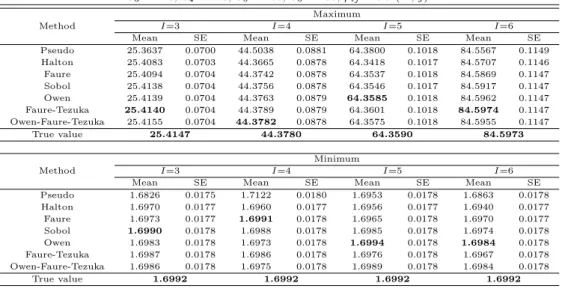
Table 4.4 Mean and standard error estimates of maximum and minimum for σ

i

= 0.2, S

1

= 80, S

2

= 100, S

₃

= 120, S

₄

= 140, S

₅

= 160, S

₆

= 180, ρ

_ij

= 0.9 (∀i, j)

Maximum

Pseudo 25.3637 0.0700 44.5038 0.0881 64.3800 0.1018 84.5567 0.1149 Halton 25.4083 0.0703 44.3665 0.0878 64.3418 0.1017 84.5707 0.1146 Faure 25.4094 0.0704 44.3742 0.0878 64.3537 0.1018 84.5869 0.1147 Sobol 25.4138 0.0704 44.3756 0.0878 64.3546 0.1017 84.5917 0.1147 Owen 25.4139 0.0704 44.3763 0.0879 64.3585 0.1018 84.5962 0.1147 Faure-Tezuka 25.4140 0.0704 44.3789 0.0879 64.3601 0.1018 84.5974 0.1147 Owen-Faure-Tezuka 25.4155 0.0704 44.3782 0.0878 64.3575 0.1018 84.5955 0.1147

True value 25.4147 44.3780 64.3590 84.5973

Minimum

Pseudo 1.6826 0.0175 1.7122 0.0180 1.6953 0.0178 1.6863 0.0178 Halton 1.6970 0.0177 1.6960 0.0177 1.6956 0.0177 1.6940 0.0177

Faure 1.6973 0.0177 1.6991 0.0178 1.6965 0.0178 1.6970 0.0177

Sobol 1.6990 0.0178 1.6988 0.0178 1.6985 0.0178 1.6974 0.0178

Owen 1.6983 0.0178 1.6973 0.0178 1.6994 0.0178 1.6984 0.0178

True value 1.6992 1.6992 1.6992 1.6992

상관계수가 0.5인 경우를 살펴보면 자산의 가격이 동일하였던 앞의 경우와 마찬가지로 최대값의 경우 에는 혼합법들 중 하나의 추정치가 가장 정확하였으며 최소값의 경우에도 혼합법들 중 하나가 가장 정확 한것으로 나타났다. 상관계수가 0.9로 큰 경우에는 최소값의 경우 자산이 3개인 경우에는 Sobol 준난 수가, 4개인 경우에는 Faure 준난수를 사용하는 것이 가장 정확한 것으로 나타났다. 결과적으로 상관계 수가 높은 경우 최소값에 대하여 임의 준난수를 사용하는 혼합법들의 효과가 상대적으로 떨어지는 것을 볼 수 있다. 기초자산의 가격이 다른 경우에도 자산의 수가 커질수록 Halton 수열의 경우 추정치의 오 차가 커지는 것을 확인할 수 있었다.

5. 결론

본 논문에서는 저불일치 수열인 준난수들을 이용하는 준몬테칼로 방법이 다중자산 옵션의 최대값과 최소값에 대한 가격을 추정하는데 어떤 영향을 미치는지 시뮬레이션을 이용하여 비교하였다. 옵션의 행 사가격, 무위험 이자율, 잔존 만기시점 값들은 고정된 값들을 사용하였으며 자산의 표준편차, 자산들 사 이의 상관계수, 자산의 수와 가격들에 대한 여러 조합을 사용하였다. 정규난수의 경우에는 정확성을 높 이기 위하여 모로 역변환을 적용하였으며 반복수는 준난수 방법들이 수렴하는 정도를 참고하여 모든 경 우에 100,000번으로 고정하여 기본적인 몬테칼로 방법들과의 차이를 살펴보았다.

전체적으로 기본적인 몬테칼로 방법에 비하여 준난수를 이용하는 방법들의 정확성이 높았고 이들 중 혼합법들의 정확도가 대부분의 경우에 있어 더욱 높은 것으로 나타났으나 혼합법들 간의 차이는 거의 없 는것으로 판단된다. 하지만, 최소값의 경우 자산사이의 상관계수가 높고 가격이 모두 다를 때에는 혼 합법들의 효과가 떨어져 Faure 또는 Sobol 방법들의 추정치가 가장 정확하게 나타나기도 하였다. 특히, 자산의 표준편차가 상대적으로 큰 경우에는 자산의 수가 많은 경우 높은 상관관계를 보이는 문제점을 가 지고 있는 Halton 수열의 경우 추정치와 이론가격의 차이가 급격하게 커지는 것을 볼 수 있었다.

결과적으로 준몬테칼로 방법들과 다양한 혼합법들을 사용하면 기본적인 몬테칼로 방법에 비교하여 상 대적으로 높은 정확성을기대할 수 있으며 특히 여러 혼합법들이 자산의 수나 상관계수 등에 큰 영향을 받지 않고 정확한 추정치를 나타내는 것을 알 수 있었다. 여러 방법들의 우열에 대한 명확한 판단을 위 하여 더욱 다양한 요인들의 조합에 대한 시뮬레이션 연구가 필요하다고 하겠다.

(8)

References

Antonov, I. A. and Saleev, V. M. (1979). An economic method of computing LP-sequences. USSR Journal of Computational Mathematics and Mathematical Physics, 19, 252-256.

Beasley J. D. and Springer, S. G. (1977). Algorithm AS 111 : The percentage points of the normal distribution. Journal of the Royal Statistical Society C, 26, 118-121.

Boyle, P., Evnine, J. and Gibbs, S. (1989). Numerical evaluation of multivariate contingent claims. Riview of Financial Studies, 2, 241-250.

Cox, J. and Ross, S. A. (1976). The valuation of options for alternative stochastic processes. Journal of Financial Economics, 3, 145-166.

Faure, H. (1982). Discr` epance de suites associ´ ees ` a un syst´ eme de numerations (en dimensions). Acta Arith, 41, 337-351.

Faure, H. and Tezuka, S. (2002). Another random scrambling of digital (t, s)-sequences. In Monte Carlo and Quasi-Monte Carlo Methods, Springer, Berlin, 242-256.

Galanti, S. and Jung, A. (1997). Low-discrepancy sequences : Monte Carlo simulation of option prices.

Journal of Derivatives, 5, 63-83.

Halton, J. (1964). Algorithm 247: Radical-inverse quasi-random point sequence. ACM, 7, 701-702.

Hong, H. S. and Hickernell, F. J. (2003). Algorithm 823 : Implementing scrambled digital sequences. ACM Transactions on Mathematical Software, 29, 95-109.

Joe, S. and Kuo, F. Y. (2003). Remark on algorithm 659: Implementing Sobol’s quasirandom sequence generator. ACM Transactions on Mathematical Software, 29, 49-57.

Johnson, H. (1981). The pricing of complex options, Unpublished manuscript.

Johnson, H. (1987). Options on the maximum or the minimum of several assets. Journal of Financial and Quantitative Analysis, 22, 277-283.

Levy, G. (2004). Computational finance numerical methods for pricing financial instruments, Elsevier, Oxford.

Margrabe, W. (1978). The value of an option to exchange one asset for another. Finance, 33, 177-186.

Moro, B. (1995). The full monte. Risk, 8, 57-58.

Owen, A. B. (1995). Randomly permuted (t,m,s)-nets and (t,s)-sequences. In Monte Carlo and Quasi- Monte Carlo Methods in Scientific Computing, edited by H. Niederreiter and P. J. S. Shiue, Springer- Verlag, New York, 299-317.

Sobol, I. M. (1967). The distribution of points in a cube and the approximate evaluation of integrals. USSR Journal of Computational Mathematics and Mathematical Physics, 7, 86-112.

Stulz, R. M. (1982). Options on the minimum or maximum of two risky assets : Analysis and applications.

Journal of Financial Economics, 10, 161-185.

Wu, X. and Zhang, J. E. (1999). Options on the minimum or the maximum of two average prices. Review

of Derivatives Research, 3, 183-204.

(9)

2013, 24

(

4)

,

669–677

Application of quasi-Monte Carlo methods in multi-asset option pricing

Eun Bi Mo

¹

· Chongsun Park

²

12Department of Statistics, Sungkyunkwan University

Received 3 May 2013, revised 24 May 2013, accepted 29 May 2013

Abstract

Quasi-Monte Carlo method is known to have lower convergence rate than the standard Monte Carlo method. Quasi-Monte Carlo methods are using low discrepancy sequences as quasi-random numbers. They include Halton sequence, Faure sequence, and Sobol sequence. In this article, we compared standard Monte Carlo method, quasi- Monte Carlo methods and three scrambling methods of Owen, Faure-Tezuka, Owen- Faure-Tezuka in valuation of multi-asset European call option through simulations.

Moro inversion method is used in generating random numbers from normal distribution. It has been shown that three scrambling methods are superior in estimating option prices regardless of the number of assets, volatility, and correlations between assets. However, there are no big differences between them.

Keywords: Moro inversion, multi-asset option, quasi-Monte Carlo, quasi-random numbers.

1

Graduate student, Department of Statistics, Sungkyunkwan University, Seoul 110-745, Korea.

2

Corresponding author: Professor, Department of Statistics, Sungkyunkwan University, Seoul 110-745,

Korea. E-mail: cspark@skku.edu