Study of the Critical Behavior of the Ising Model on a Kagomé Lattice
Seung-Yeon Kim
School of Liberal Arts and Sciences, Korea National University of Transportation, Chungju 27469, Korea
Wooseop Kwak
∗Department of Physics, Chosun University, Gwangju 61452, Korea (Received 21 March 2018 : revised 24 April 2018 : accepted 7 May 2018)
We numerically investigate the second-order phase transition of the ferromagnetic Ising model on a two-dimensional kagomé lattice. The critical behavior of this model is studied using Wang- Landau entropic sampling, and the joint density of states is obtained as a function of the energy and the magnetization. The partition function, which is a function of temperature, is calculated using the joint density of states. Using the partition function, we found a critical point and a thermodynamic function, such as the specic heat and the magnetic susceptibility, at the critical point, and by using finite-size scaling, we obtained the critical exponents in the thermodynamic limit, with those exponents satisfiying the hyperscaling relations.
PACS numbers: 05.10.-a, 05.10.Ln, 02.70.Uu
Keywords: Ising model, Joint density of states, Kagomé lattice, Wang-Landau entropic sampling
카고메 격자 위의 이징 모형의 임계현상 연구
김승연
한국교통대학교 교양학부, 충주 27469, 대한민국
곽우섭
∗조선대학교 자연과학대학 물리학과, 광주 61452, 대한민국
(2018년 3월 21일 받음, 2018년 4월 24일 수정본 받음, 2018년 5월 7일 게재 확정)
이차원 카고메 (Kagomé) 격자 위의 강자성 이징 모형의 임계현상을 엔트로피 표본잡기 (entropic sampling) 를 이용하여 연구하였다. 왕-란다우 엔트로피 표본잡기 (Wang-Landau entropic sampling) 를 이용하여 얻은 에너지와 질서맺음변수 (order parameter) 의 결합 상태밀도 (joint density of states) 를 이용하여 온도의 함수인 분배함수 (partition function) 를 계산하였다. 분배함수를 이용하여 임계점 (critical point) 을 구하고 임계점에서 비열 (specific heat) 등의 열역학 함수 (thermodynamic function) 를 얻었으며, 유한축적 법칙 (finite size scaling) 을 이용하여 열역학적 극한 (thermodynamic limit) 에서의 열역학 함수의 임계현상을 탐구하였다.
PACS numbers: 05.10.-a, 05.10.Ln, 02.70.Uu
Keywords: 이징 모형, 결합 상태밀도, 카고메 격자, 왕-란다우 엔트로피 포본잡기
∗E-mail: wkwak@chosun.ac.kr
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
I. 서 론
통계물리학에서 몬테카를로 전산시늉 (Monte Carlo sim- ulation) 은 상전이현상과 임계점에서 임계현상 연구에 중 요한 역할 [1–26]을 하고 있다. 컴퓨터에서의 계산 성능을 향상 시키고 정확한 결과를 얻기 위하여 히스토그램 재가 중 방법 (histogram reweighting method) [1–3,12,13], 일 반화된 앙상블 방법 (generalized ensemble method) [16, 20–22], 엔트로피 무작위 표본추출 방법 (entropy sampling method) [4,15,23–31] 등이 연구 개발되고 있다.
정확히 상전이 점을 찾아내고 상전이 점에서 임계현상 (critical phenomena) 을 연구하는데 히스토그램 재가중 방 법과 엔트로피 무작위 표본 추출 방법 등이 사용되어 왔다.
그중에서 엔트로피 무작위 표본 추출은 온도에 의존하지 않기 때문에 낮은 온도에서 전산시늉을 할 수 있고, 이러한 엔트로피 무작위 표본 추출 방법들 중에 왕-란다우 무작위 표본 추출 방법 (Wang-Landau sampling method) [4]이 소 개된 이후로, 이 방법의 놀라운 확장성으로 인하여 활발히 사용되고 있다. 특히, 이 방법은 완화시간 (relaxation time) 이 오래 걸리는 전산시늉 모형에서 계산시간을 단축하고 직접 자유에너지, 엔트로피, 상태밀도 등을 구할 수 있는 엔트로피 무작위 표본 추출 방법이다.
이징 모형 (Ising model) 은 이차원, 삼차원 그리고 초입 방격자 (hyper square lattice) 에서 모두 이차 상전이 현상 (second-order phase transition)을 보이며, 4차원보다 크면 평균장이론 (mean-field theory) 을 따른다. 그래서 4차원은 상임계 차원 (upper critical dimension) 으로 알려져 있다.
이 논문에서는 이차원 카고메 (kagomé) 격자 [32] 위의 강자성 이징 모형의 임계현상을 연구하기 위하여 왕-란다우 표분 추출방법으로 결합 상태밀도 (joint density of states) 를 구하고, 결합 상태밀도로부터 얻은 분배함수 (partition function) 로 유한크기의 임계점 (finite-size critical point) 에서 비열 (specific heat) 과 자기감수율 (magnetic suscep- tibility) 과 같은 열역학적 함수 (thermodynamic function) 를 얻어서, 유한축척 법칙 (finite-size scaling theory) 을 이 용하여 열역학적 극한 (thermodynamic limit) 에서 임계현 상을 탐구하였다.
II. 연구 방법 및 이론
1. 모형
강자성 (ferromagnetic) 이징 모형의 해밀토니안은 다음 과 같다.
H = −JE − hM, (1)
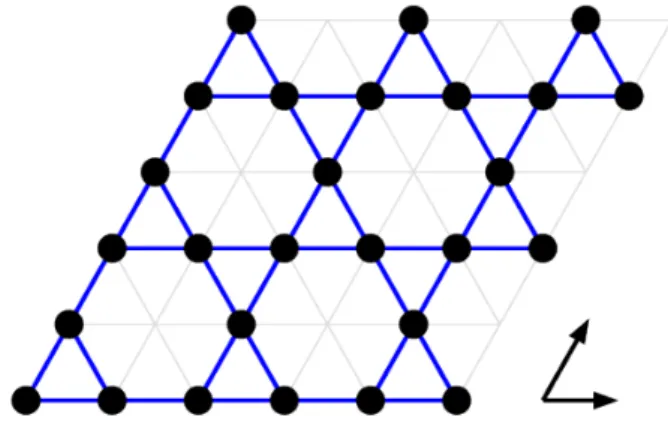
Fig. 1. (Color online) Schematic plot of 6× 6 kagomé lattice.
여기서 결합에너지 E = ∑
<i,j>SiSj 이고 자기화 M =
∑
iSi이며 이징 모형의 스핀이 +z 축으로 정렬되어 있으면 Si= 1이고, 반대 방향으로 정렬되어 있으면 Si=−1이고 스핀의 합은 최인접이웃 (nearest neighbors) 에 대해서만 수 행된다. 강자성 이징 모형의 결합상수 (coupling constant) 인 J 는 0 보다 큰 상수이며, h 는 외부 자기장이다.
2. 카고메 격자
삼각 격자 (triangular lattice) 와 벌집 격자 (honeycomb lattice) 의 결합한 모양인 카고메 격자는 Syozi [32]에 의하 여 처음으로 소개되었다. 이차원 평방 격자 (square lattice) 와 같이 좌표수 (coordination number) 가 4 인 카고메 격자 는 기하학적 자기 스핀 쩔쩔맴 (geometrical magnetic spin frustration) 현상을 연구하는데 물리학, 화학, 공학 분야에 서 중요한 역할을 하고 있다. 강자성 이차원 카고메 격자는 널리 연구가 되어 왔지만 아직도 임계점에서 나타나는 물 리현상은 잘 알려지 있지 않다. Fig. 1은 일반적인 카코메 격자의 개략도를 보여주고 있다.
3. 왕-란다우 무작위 표본 추출 방법
무작위로 스핀을 선택하여 계의 상태를 변화하며 에너지 공간에서 무작위 걸음을 하는 왕-란다우 무작위 표본 추출 방법은 전이확률 (transition probability) 이 단지 결합 상 태밀도에만 의존하므로, 에너지 E1과 질서맺음변수 (order parameter) M1을 가진 상태 S1에서 에너지 E2와 질서맺 음변수 M2를 가진 상태 S2로의 전이확률은 다음과 같이 쓸 수 있다 :
p (S1→ S2) = min
(g(E1, M1) g(E2, M2), 1
)
, (2)
g(E1, M1)≥ g(E2, M1)이면 min g(Eg(E1,M1)
2,M2), 1 = 1이므 로 전이확률 p = 1 이 되어서 새로운 에너지 E2와 새로운 질서맺음변수 M2를 갖는 새로운 상태가 항상 선택이 되고, 만일 g(E1, M1) < g(E2, M2)이면 전이확률 p = g(Eg(E1,M1)
2,M2)
에 따라 새로운 상태가 선택되어진다.
전산시늉을 하는 동안 에너지 히스토그램 (histogram) H(E, M )과 수정인자 (modification factor) f 를 사용한 상태밀도 g(E, M ) 를 구하여 계속 축척시킨다. 여기서 축 척시키는 방법은 다음과 같다 :
H(E2, M2) → H(E1, M1) + 1 (3) g(E2, M2) → g(E1, M1)× f (4) 여기서, 초기 finitial= e1을 사용한다. 에너지 공간을 무작 위 걸음을 통하여 에너지 히스토그램이 평평해지면 히스토 그램 H(E, M ) 를 전부 0 으로 재설정하고, 새로운 수정인자 fi+1 = fi1/2로 바꾸어, 최종 수정인자가 ffinal = e−9가 될 때까지 전산시늉을 수행하여 결합상태밀도 g(E, M ) 를 구한다.
4. 물리량
상태밀도 g(E, M ) 를 알면, 온도 T 에 의존하는 분배함수 는
Z(T, h) = ∑
E,M
g(E, M )eβJ EeβhM (5)
이고, 여기서 β = 1/kBT는 역온도 (inverse temperature) 이다. 비열 c 는
c = kBβ2 L2
∂logZ
∂β2 , (6)
이고 자기감수율 χ 는 χ(T ) = lim
h→0
∂2
∂h2 [
−kBT
L2 ln Z (T, h) ]
(7) 로 정의 된다. 임계점 Tc에서 비열은 열역학적 극한에서 다음과 같이,
c(T )∼ |T − Tc|−α, (8) 발산하고 자기감수율 χ 는
χ(T )∼ |T − Tc|−γ, (9) 에 따라 발산한다. 상관관계 길이 (correlation length) ξ(T ) 는 열역학적 극한에서
χ(T )∼ |T − Tc|−ν, (10)
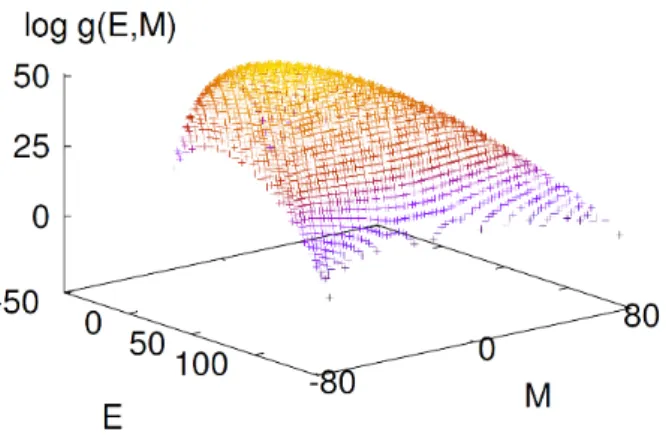
Fig. 2. (Color online) Plot of log (g(E, M )) as a function of interaction energy E and magnetization M for Ising model on 10× 10 kagomé lattice.
이다. 위의 식에서
|T − Tc| ∼ ξ−1/ν (11) 이므로, 유한한 크기의 시스템에서 상관관계 길이 ξ = L 이므로,
c(T )∼ Lα/ν (12)
이고,
χ(T )∼ Lγ/ν (13)
이다.
III. 결과 및 고찰
정확한 결합 상태밀도를 구하기 위하여서 전산시늉은 많은 시간이 소요된다. 정확도를 높이기 위하여 히스토 그램의 평편도 (flatness) 를 99% 로 높이고 시스템의 크기 L = 8, 10, 12, 14, 16와 18 인 카고메 격자위의 이징모형에서 전산시늉이 수행되었다.
Fig.2는 일반적인 형태를 보여주기 위한 예시로써 10×10 카고메 격자위의 결합 상태밀도를 보여주고 있다. 여기서 결합 상태밀도는 매우 크기 때문에 에너지 E 와 자기화 M 에 대응하는 결합 상태밀도에 로그 (log) 를 취하여 계산하였다.
Fig.3에서 이차원 카고메 격자 위의 이징 모형의 비열이 시 스템 크기 L 에 비례하여 증가하는 경향성을 보여주고 있다.
Fig.4는 시스템 크기에 따라 이차원 카고메 격자 위의 이징 모형의 자기 감수율이 시스템 크기 L 에 비래하여 증가하는 경향성을 보여주고 있다. Fig. 5에서 이차원 카고메 격자 위의 이징 모형의 유한크기의 임계점에서 비열의 최대값을
Fig. 3. (Color online) Plot of specific heat c(T ) as a function of temperature T .
Fig. 4. (Color online) Plot of magnetic susceptibility χ(T ) as a function of temperature T .
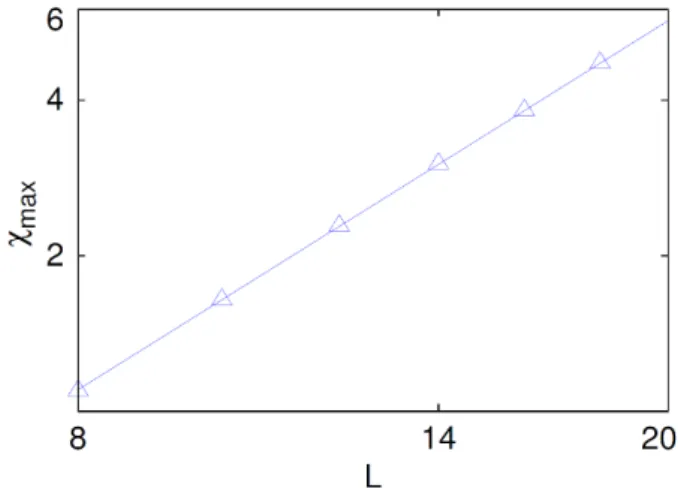
시스템의 크기 L 의 함수로 보여주고 있다. 여기서 기울기는 α/ν = 0.39(3)이다. Fig. 6에서 이차원 카고메 격자 위의 이징 모형의 유한크기의 임계점에서 자기감수율의 최대값을 시스템의 크기 L 의 함수로 보여주고 있다. 여기서 기울기는 γ/ν = 1.795(10)이다.
IV. 논의 및 결론
우리는 이차원 카고메 격자 위의 강자성 이징 모형의 임계 현상을 왕-란다우 엔트로피 표본잡기를 이용하여 얻은 결합 상태밀도를 이용하여 온도의 함수인 분배함수를 처음으로 계산하였다. 분배함수를 이용하여 유한크기에서 비열과 자기감수율의 최대값을 구한 후, 유한축적 법칙을 이용하 여 임계지수 α/ν = 0.39(3) 와 임계지수 γ/ν = 1.795(10) 을 구하였다. 이들 두 임계지수들로부터 구한 열축적지수 (thermal scaling exponent) 는 yt = 1.195(15)이고, 자기
Fig. 5. (Color online)Plot of maximum values of finite- size specific heat cmax as a function of linear dimension L.
Fig. 6. (Color online) Plot of maximum values of finite- size magnetic susceptibility χmaxas a function of linear dimension L.
축적지수 (magnetic scaling exponent) 는 yh= 1.898(5)이 다. 이렇게 구한 축척지수들로부터 질서맺음변수 임계지수 β = 0.086(6)와 상관관계 길이 임계지수 ν = 0.837(11) 를 얻을 수 있었다. 이 값들은 초눈금잡기관계식 (hyperscaling relation) α+2β +γ = 2.00(7) 로 잘 만족하고 있다. 우리의 결과는 강자성 이징 모형의 보편화군 가설이 잘 맞는다는 것을 명확하게 보여주고 있다.
감사의 글
이 논문은 2017년도 한국연구재단의 지원을 받아 수행된 연구입니다 [곽우섭 NRF-2017R1A2B1008259 및 김승연 NRF-2017R1D1A3B06035840].
REFERENCES
[1] Computer Simulation Studies in Condensed Matter Physics II, edited by D. P. Landau, K. K. Mon and H.-B. Schüttler (Springer-Verlag, Berlin, 1990).
[2] A. M. Ferrenberg and D. P. Landau, Phys. Rev. B 44, 5081 (1991).
[3] K. Chen, A. M. Ferrenberg and D. P. Landau, Phys.
Rev. B 48, 3249 (1993).
[4] F. Wang and D. P. Landau, Phys. Rev. Lett. 86, 2050 (2001).
[5] A. M. Ferrenberg, D. P. Landau and R. H. Swend- sen, Phys. Rev. E 51, 5092 (1995).
[6] K. Binder, Computational Methods in Field Theory, edited by C. B. Lang and H. Gausterer (Springer, Berlin, 1992).
[7] K. Binder and D. W. Heermann, Monte Carlo Simu- lation in Statistical Physics (Springer, Berlin, 1992).
[8] W. Kwak, D. P. Landau and B. Schmittmann, Phys.
Rev. E 69, 66134 (2004).
[9] W. Kwak and D. P. Landau, Int. J. Mod. Phys. C 17, 15 (2006).
[10] W. Kwak, J.-S. Yang and I.-M. Kim, Phys. Rev. E 75, 41108 (2007).
[11] W. Kwak, J.-S. Yang, J.-i. Sohn and I.-M. Kim, Phys. Rev. E 75, 61110 (2007).
[12] W. Kwak, J.-S. Yang, J.-i. Sohn and I.-M. Kim, Phys. Rev. E 75, 61130 (2007).
[13] W. Kwak, J.-S. Yang, K.-I. Goh and I.-M. Kim, Eu- rophys. Lett. 84, 36004 (2008).
[14] J-S. Yang, I.-M. Kim and W. Kwak, Europhys. Lett.
88, 20009 (2009).
[15] W. Kwak and U. H. Hansmann, Phys. Rev. Lett.
95, 138102 (2005).
[16] J.-S. Yang and W. Kwak, Comput. Phys. Commun.
181, 99 (2010).
[17] H. E. Stanley, D. Stauffer, J. Kertesz and H. J. Her- rmann, Phys. Rev. Lett. 59, 2326 (1987).
[18] H. J. Herrmann, Physica A 168, 516 (1990).
[19] F. Wang, N. Hatano and M. Suzuki, J. Phys. A:
Math. Gen. 28, 4543 (1995).
[20] E. Marinari and G. Parisi, Europhys. Lett. 19, 451 (1992).
[21] U. H. E. Hansmann, Chem. Phys. Lett. 281, 140 (1997).
[22] V. Aleksenko, W. Kwak and U. H. E. Hansmann, Physica A 350, 28 (2005).
[23] B. A. Berg and T. Neuhaus, Phys. Rev. Lett. 68, 9 (1992).
[24] B. A. Berg, Int. J. Mod. Phys. C 4, 249 (1993).
[25] P. M. C. de Oliveira, T. J. P. Penna and H. J. Her- rman, Braz. J. Phys. 26, 677 (1996).
[26] J.-S. Wang, Physica A 281, 147 (2000).
[27] G. Bhanot, R. Salvador, S. Black, P. Carter and R.
Toral, Phys. Rev. Lett. 59, 803 (1987).
[28] J. Lee, Phys. Rev. Lett. 71, 211 (1993).
[29] S.-Y. Kim and W. Kwak, J. Korean Phys. Soc. 65, 436 (2014).
[30] S.-Y. Kim, J. Korean Phys. Soc. 67, 423 (2015).
[31] S.-Y. Kim, J. Korean Phys. Soc. 70, 561 (2017).
[32] I. Syozi, Prog. Theor. Phys. 6, 306 (1951).