유한요소법에 의한 비등방성 두꺼운 원통형 쉘 및 얇은 원통형 쉘의 비교 해석
A Comparative Analysis of Anisotropic Thick Cylindrical Shells and Anisotropic Thin Cylindrical Shells by Finite Element Method
김기동 Kim, Gi-Dong* · 박원태 Park, Weon-Tae **†
(Received August 10, 2010 ; Revised September 1, 2010 ; Accepted September 2, 2010) ABSTRACT
This paper is presented for the analysis results of the bending problems of the anisotropic cylindrical shells. In the numerical analysis of various mechanical problems involving complex partial differential equations, Finite element method is used to analyze the governing equations of anisotropic cylindrical shells. Both thin shell theory and thick shell theory are used as the basic governing equations of bending problems in the anisotropic cylindrical shells. The analysis results are compared between the anisotropic thick cylindrical shells and the anisotropic thin cylindrical shells. The results of this study will be contribute to analyze the bending behavior of anisotropic cylindrical shells.
요 지
본 연구는 비등방성 원통형 쉘의 휨문제에 대한 해석 기법을 제시하였다. 비등방성 원통형 쉘의 지배방정식을 해석 하기 위해 유한요소법을 사용하였다. 두꺼운 쉘이론과 얇은 쉘이론을 사용하여 쉘의 폭-두께비 및 여러 가지 경계 조건을 갖는 비등방성 원통형 쉘에 대한 해석결과를 비교 분석하였다. 본 연구의 수치해석 결과는 비등방성 원통형 쉘의 휨 거동 분석에 기여할 것으로 보인다.
Key Words: Anisotropic thick cylindrical shell(비등방성 두꺼운 원통형 쉘), Anisotropic thin cylindrical shell(비등방성 얇은 원통형 쉘), Finite element metho(유한요소법)
1. 서 론
대규모의 저수탱크나 하수처리 탱크 혹은 액체의 대량 저장에 잘 쓰이는 원형 원통형 쉘구조는 그 형상이 좋 고 시공이 쉬우며 다른 형식의 쉘구조에 비하여 역학 적으로 안정되고 또한 경제적이다. 그러나 이러한 원 형 원통형 쉘구조물은 해석적인 방법으로는 그 응력을 알아낸다는 것은 극히 어렵다. 본 연구에서는 원형 원 통형 쉘구조에 대하여 실용적인 견지에서 충분히 정확 한 해를 얻기 위하여 유한요소법을 적용하려 한다. 또 한 쉘구조의 재료로서는 강재나 콘크리트가 대부분을 차지하고 있으나 최근에는 경제적이고 더 강한 대체 재료로써 복합재료가 연구, 개발되고 있다. 복합재료는 그 자체 중량에 비하여 강성, 강도및 내구성등이 탁월 한 다양한 소재로 구성되어 하나의 구조체를 형성한 다. 기존의 보와 판에 전단변형효과를 고려한 연구에 추가하여(장석윤, 윤석호 1992; 장석윤, 이원홍 1992) 본 연구에서는 쉘 설계자들에게 유한요소법에 의한 얇
은 쉘 이론과 두꺼운 쉘이론에 의한 비등방성 원통형 쉘의 해석과정의 이론적 이해를 돕기 위하여, 여러 가 지 경계조건을 갖는 복합재료로 구성된 비등방성 원통 형 쉘구조물을 모델로 하여 전단변형효과를 무시한 얇은 쉘이론과 전단변형효과를 고려한 두꺼운 쉘이론 에 의한 해석결과를 비교 검토하였다.
2. 기본 이론
2.1 쉘의 변위벡터와 변형률벡터Actual deformation x, u
z, w θ, v βθ
βx Φx
∂w∂x Φθ
∂w/∂θ
Thick cylindrical shell theory
Thin cylindrical shell theory
Actual deformation x, u
z, w θ, v βθ
βx Φx
∂w∂x Φθ
∂w/∂θ
Thick cylindrical shell theory
Thin cylindrical shell theory x, u
z, w θ, v βθ
βx Φx
∂w∂x Φθ
∂w/∂θ
Thick cylindrical shell theory
Thin cylindrical shell theory
Fig. 1 원통형 쉘의 변위
쉘에 대한 좌표를 직각 곡선좌표계를 사용하여 쉘 길이방향을 x, 원주방향을 θ, 원의 반경방향을 z라 정 의하여, 미소 쉘요소의 각 방향의 변위를u, v, w 라 하고, 처짐에 의한 각 변위를βx,βθ라 하면 Fig. 1과 같이 나타낼 수 있다. 전단변형효과를 무시한 얇은 쉘이론에 의한 비등방성 원통형 쉘의 변위 벡터
(δCSK) 및 변형률 벡터(εCSK)와 전단변형효과를 고 려한 두꺼운 쉘이론에 의한 비등방성 원통형 쉘의 변 위 벡터( δCSM) 및 변형률 벡터( εCSM)와 각각 식 (1)
∼(4)와 같이 나타낼 수 있다(Robert M. Jones, 1975;
H. Marshall, 1981; J. N. Reddy, 1981; Eduard Ventsel Theodor Krauthammer, 2001).
δCSK==
uv
∂ww
∂x
∂w
∂θ
=
uv w βx βθ
(1)
δCSM=
uv
∂ww
∂x+φx
∂w
∂θ +φθ
=
uv w βx βθ
(2)
εCSK=
{
εεε000xθxθ}
+{
κκκxθxθ}
CSK (3) εCSM={
εεε000xθxθ}
+{
κκκxθxθ}
CSM(4)
여기서,
ε0=
{
εεε000xθxθ}
=
∂u
∂x R1 ∂v
∂θ + 1 1 R w R ∂u
∂θ + ∂v
∂x
(5)
κCSK=
{
κκκθxxθ}
CSK=
∂ βx
∂x R1 ∂ β∂θθ R1 ∂ β∂θ +x ∂ βθ
∂x
(6)
κCSM=
{
κκκθrxθ}
CSM=
∂ βx
∂x R1 ∂ β∂θθ R1 ∂ β∂θ +x ∂ βθ
∂x
(7)
{
γγθxzz}
={
R1 ∂θ -∂∂w∂wx-βRvx+βθ}
(8) 여기서, ε0x, ε0θ, ε0xθ는 쉘의 중면에서의 발생하 는 수직 및 전단변형률, κx, κθ, κxθ 와κx,κθ,κxθ 는 휨에 의해 발생하는 얇은 쉘이론과 두꺼운 쉘이론 에서의 곡률, γθz,γxz 는 쉘의 전단변형률을 각각 나 타낸다.2.2 단면력과 변형률관계
비등방성 원통형 쉘의 구조축에 대한 응력-변형률 관계식은 재료축의 강도를 좌표 변환하여 식 (9)~(10) 과 같이 표시할 수 있다 (Wilhelm Flugge, 1973;
Hou-Cheng Huang, 1989; J. N. Reddy, 1995).
{
τσσxθxθ}
=
Q11 Q12 Q16 Q12 Q22 Q26
Q16 Q26 Q66
{
γεεxθxθ}
(9){
ττθzxz}
=[
QQ4555 QQ4445] {
γγθzrz}
(10) 여기서, [Qij]는 비등방성 쉘의 재료축에서의 재료 강도를 구조축으로 좌표변환하여 구한 재료강도를 나 타낸다. Fig. 2의 원통형 쉘의 단면력을 얇은 쉘이론과 두꺼운 쉘이론에 의한 변형률과의 관계는 식(11)∼식 (15)와 같다.{
NNNxxθθ}
CSK= AAA121611AAA222612AAA266616{
εεεxθxθ}
+ BBB111216BBB222612BBB266616{
κκκθxxθ}
( 1 1 )
{
NNNxθxθ}
CSM= AAA111216AAA222612AAA266616{
εεεθxxθ}
+ BBB111216BBB222612BBB266616{
κκκxθxθ}
(12)
{
MMMxθxθ}
CSK=
B11 B12B16
B12 B22B26
B16A26B66
{
εεεxθxθ}
+
D11 D12D16
D12D22D26 D16D26D66
{
κκκθxxθ}
(13)
{
MMMxθxθ}
CSM= BBB111216BBB222612BBB266616{
εεεxxθθ}
+ DDD111216DDD222612DDD266616{
κκκxθxθ}
(14)
{
QQθx}
CSM= k∑N= 1⌠⌡zzKk+ 1{
ττθxzz}
dz =[
AA4445AA5545] {
γγθr zz}
CSM (15)여기서, 는 면내력강도, 는 휨-면내력강도,
는 휨강도, K는 전단보정계수를 의미하며 각각 식 (16)∼(17)과 같다.
(Aij, Bij, Dij) = ⌠⌡
+h/2
-h/2[ Qij]k(1, z, z2)dz (i, j = 1,2,6 ) (16)
Aij=K∑N
k= 1[ Qij]k(zk-zk- 1) (i, j = 4,5 ) (17)
여기서, h는 쉘의 벽두께, K=5/6 이다.
`
Fig. 2 원통형 쉘 요소의 단면력
과 비교할 때 유사한 거동을 가지나 사각형 형식보다 더 일반적인 경우라고 볼 수 있다. 본 연구에서는 자 연좌표계(r,s)를 사용하여 직각곡선좌표계(x,θ,z)와 요 소변위를 같은 보간함수(hi)로 나타낼 수 있는 4절점
“Iso-parametric 요소”를 사용하였으며, 쉘요소내의 임 의 점(x,θ)에서의 얇은 쉘이론과 두꺼운 쉘이론에 의 한 변위는 형상함수를 이용하여 요소절점의 변위로 나 타내면 식 (18)과 같다.
δCSK=
uv w βx βθ
=∑i=14Hi(r,s) δiCSK (18)
여기서,
δiCSK=
u ( r, s) v(r,s) w(r,s) βx(r,s) βθ(r,s)
=
H1(r,s) 0 0 0 0 ⋯
0 H1(r,s) 0 0 0 ⋯
0 0 H1(r,s) 0 0 ⋯
0 0 0 H1(r,s) 0 ⋯
0 0 0 0 H1(r,s) ⋯
ui vi wi βxi βθi
(19)
δCSM=
u ( r, s) v(r ,s) w(r,s) βx(r ,s) βθ(r ,s)
CSM
=∑i=14 Hi(r ,s) δiCSM (20)
δiCSM=
u ( r , s) v(r,s) w(r,s) βx(r,s) βθ(r,s)
=
H1(r,s) 0 0 0 0 ⋯
0 H1(r,s) 0 0 0 ⋯
0 0 H1(r,s) 0 0 ⋯
0 0 0 H1(r,s) 0 ⋯
0 0 0 0 H1(r,s) ⋯
ui vi wi βxi βθ
i
(21)
2.4 변형률 매트릭스
전단변형효과를 무시한 얇은 쉘이론과 전단변형효과 를 고려한 두꺼운 쉘이론에 의한 비등방성 원통형 쉘 의 변형률과 변위관계는 식(22)∼(23)과 같다.
εC S K=[ B1 , … , B4]
u ( r , s) v( r , s) w( r , s) βx(r , s) βθ (r , s)
=∑4
i= 1BiδiC S K
(22)
εCSM==[B1 ,…, B4]
u ( r, s) v(r,s) w(r,s) β (r ,s)
=∑i4
=1BiδiCSM
여기서,
[B]i=
BA 0 0
0 BF 0
0 0 BS (24)
[B]A=
-∂Hi
∂x 0
0 ∂Hi
R∂θ
∂Hi R∂θ ∂Hi
∂x
(25-1)
[B]F=
0 -∂Hi
∂x 0
0 0 -∂Hi
R∂θ 0 -∂Hi
R∂θ -∂Hi
∂x
(25-2)
[B]S=
-∂Hi
∂x -Hi 0
-∂Hi
R∂θ 0 -Hi
(25-3)
변형률 매트릭스 Bi 에 있는 형상함수Hi는 자연 좌표계(r,s)로 정의 되어 있기 때문에 극좌표계θ로 편미분하기 위해서 좌표변환을 해야한다. 형상함수의 극좌표계(x,θ)에 대한 편도함수는 Jacobian 매트릭스 를 사용하여 자연좌표계에 대한 편도함수로 나타낼 수 있다.
{
∂∂∂θ∂HHxii}
= [ ]J -1{
∂H∂∂Hrsii}
(26) 식 (26)에서 [ ]J- 1은 식(27)과 같다.[ ]J -1 = 1 detJ
∂θ∂s - ∂x∂s - ∂θ
∂r ∂x
∂r
=
[
JJ2111JJ2212]
(27)
따라서 얇은 쉘이론과 두꺼운 쉘이론에 의한 비등방 성 원통형 쉘의 변형률 매트릭스BiCSK,BiCSM은 식 (28)
∼(29)과 같이 표시할 수 있다.
BiCSK=
0 -(J11∂hi
∂r +J12∂hi
∂s) 0
0 0 -(J21∂hi
∂r +J22∂hi
∂s ) 0 -(J21∂hi
∂s +J22∂hi
∂s) -(J11∂hi
∂s +J12∂hi
∂s )
(28)
BiCSM=
0 -(J11
∂hi
∂r +J12
∂hi
∂s) 0
0 0 -(J21
∂hi
∂r +J22
∂hi
∂s )
0 -(J21∂hi
∂s+J22∂hi
∂s) -(J11∂hi
∂s +J12∂hi
∂s )
-(J11∂hi
∂r +J12∂hi
∂s ) -hi 0
-(J21∂hi
∂s +J22∂hi
∂s ) 0 -hi
(29)
2.5 요소강도 매트릭스
얇은 쉘이론과 두꺼운 쉘이론에 의한 비등방성 원통 형 쉘의 total potential energy는 식(30)∼(31)로 나타낼 수 있다.
∏
εε ε χ χ χ
-⌠⌡AqwdA (30)
∏
εε ε +Mxχx+Mθχθ+Mxθχxθ)dA
+Qxφx+QθφθdA-⌠⌡AqwdA (31)
본 연구에서의 비등방성 원통형 쉘요소 강도 매트릭 스는 전 Postretinal energy(=π)의 정류조건으로부터 구할 수 있다. 즉.
∂π∂δ = ∂ πe
∂δe = 0 (32)
결국 얇은 쉘이론과 두꺼운 쉘이론에 의한 비등방성 원통형 쉘요소 강도 매트릭스는 식(33)과 식(34)과 같 다.
KeCSK=⌠⌡AeBTCSKDCSKBCSKRdxdθ
=⌠⌡Ae([B1(CSK)B2(CSK)⋯B4(CSK)]TD[B1(CSK)B2(CSK)⋯B4(CSK)])Rdxdθ
= ⌠⌡Ae
BT1(CSK)DB1(CSK)⋯ BT1(CSK)DBT4(CSK)
⋯ ⋯ ⋯
BT4(CSK)DB1(CSK) ⋯ [BT4(CSK)4DB(CSK)8Rdxdθ
= ⌠⌡
+1
-1
⌠⌡
+1
-1BTCSKDCSKBCSK∥J∥dξdη (33)
[D]CSK=
[
DA0CSKDFCSK0]
(34)KeCSM=⌠⌡AeBTCSMDCSMBCSMRdxdθ
=⌠⌡Ae([B1(CSM)B2(CSM)⋯B4(CSM)]TD[B1(CSM)B2(CSM)⋯B4(CSM)])Rdxdθ
= ⌠⌡Ae
BT1(CSM)DB1(CSM)⋯ BT1(CSM)DBT4(CSM)
⋯ ⋯ ⋯
BT4(CSM)DB1(CSM) ⋯ [BT4(CSM)8DB(CSM)4Rdxdθ
=⌠⌡
+1
-1
⌠⌡
+1
-1BTCSMDCSMBCSM∥J∥dξdη
=⌠⌡
+1
-1
⌠⌡
+1
-1([B1(CSM)B2(CSM)⋯B4(CSM)]TD[B1(CSM)B2(CSM)⋯B4(CSM)] ∥) J∥dξdη
= ⌠⌡
+1
-1
⌠⌡
+1
-1BTCPMDCPMBCPM∥J∥dξdη (35)
[D]CSK=
[
DACSM0 DFCSM0]
(36)[D]CSM=
DACSM 0 0 0 DFCSM 0
0 0 DSCSM (37) 한편, 식 (33)과 (35) 중에서BTCSKDCSKBCSK∥J∥dξdη,
BTCSMDCSMBCSM∥J∥dξdη는 대단히 복잡하기 때문에 직접 적분하지 않고 수치적분을 하게 되며 일반적으로 식 (38)과 같은 Gauss-Legendre의 구적법을 사용한다.
Ⅱ= ⌠⌡
-1
+1
⌠⌡
-1
+1K(ξ,η)dξdη
=⌠⌡
-1
+1∑n
+1wiK(ξi,η)dη=⌠⌡
-1
+1φ(η)dη
=∑in
=1φ(ηi)=∑in
=1∑in
=1wiwjK(ξi,ηj) (38) 여기서, ξi, ηj는 i, j번째 Gauss point의 ξ,η의 좌 표이다.
3. 수치해석의 적용
본 연구의 해석방법에 의한 수치해석을 위해 원통 형 쉘 구조물을 Fig. 3 같이 모델링을 하여, Table 1 에서와 같은 재료의 물성치를 사용하여 해석하였다.
Fig. 3 원통형 쉘의 해석모델
Table 1 등방성재료 및 비등방성재료의 물성치 engineering constants isotropic material
E = 3×106kN/m2,
m, m, L = 300 m
anisotropic materials
. × KN/m2, . × kN/m2
. × kN/m2
. × kN/m2
. × kN/m2
ν=,ν=
Table 2 얇은 쉘 이론 및 두꺼운 쉘 이론에 의한 등방 성 원통형 쉘의 최대변위(Dz) (강영주 등, 2003)
Vertical displacement (Dz)(m)
MIDAS/CIVIL (version 6.1.1)
Table 2 에서는 해석결과의 타당성을 알아보기 위해 등방성 원통형 쉘의 최대변위를 얇은 쉘이론 및 두꺼 운 쉘이론에 의한 해석결과를 해석해와 비교 검토하였 다. 두꺼운 쉘이론에 의한 해석결과에서는 쉘의 최대 변위(Dz)가 이론적 해석해와 약 3.455%차이를 보이며, 얇은 쉘이론에 의한 해석결과에서는 이론적 해석해와 약 9.98%의 차이를 나타내었다.
Fig. 4는 Table 1의 재료 물성치를 사용하여 4변 단 순지지된 등방성 원통형 쉘의 얇은 쉘이론과 두꺼운 쉘이론에 의한 쉘 전체에 대한 해석결과를 제시하였 다.
Fig. 4 등방성 원통형 쉘의 변위(Dz)
Table 3 4변이 단순지지 조건인 비등방성 원통형 쉘의 폭-두께비(t/a)에 따른 최대 변위(Dz).
폭-두께비(t/L) Thick Shell theory
Thin
shell theory 차이(%)
0.001 0.02742 0.02741 0
0.01 0.01277 0.01263 1.1
0.02 0.00910 0.00790 13.2
0.04 0.00544 0.00311 42.8
0.06 0.00412 0.00158 61.7
0.08 0.00351 0.00096 72.6
0.10 0.00317 0.00065 79.5
0.15 0.00275 0.00034 87.6
0.2 0.00256 0.00023 91.0
Table 3은 비등방성 원통형 쉘의 얇은 쉘 이론과 전단변형을 고려한 두꺼운 쉘 이론에 의한 쉘의 폭-두 께비에 따른 최대처짐의 해석결과를 나타내었다. 폭-두 께비가 0.02이상에서는 13.2%이상의 차이를 보이고 있 다. 따라서 폭-두께비가 0.02이상의 쉘의 해석에서는
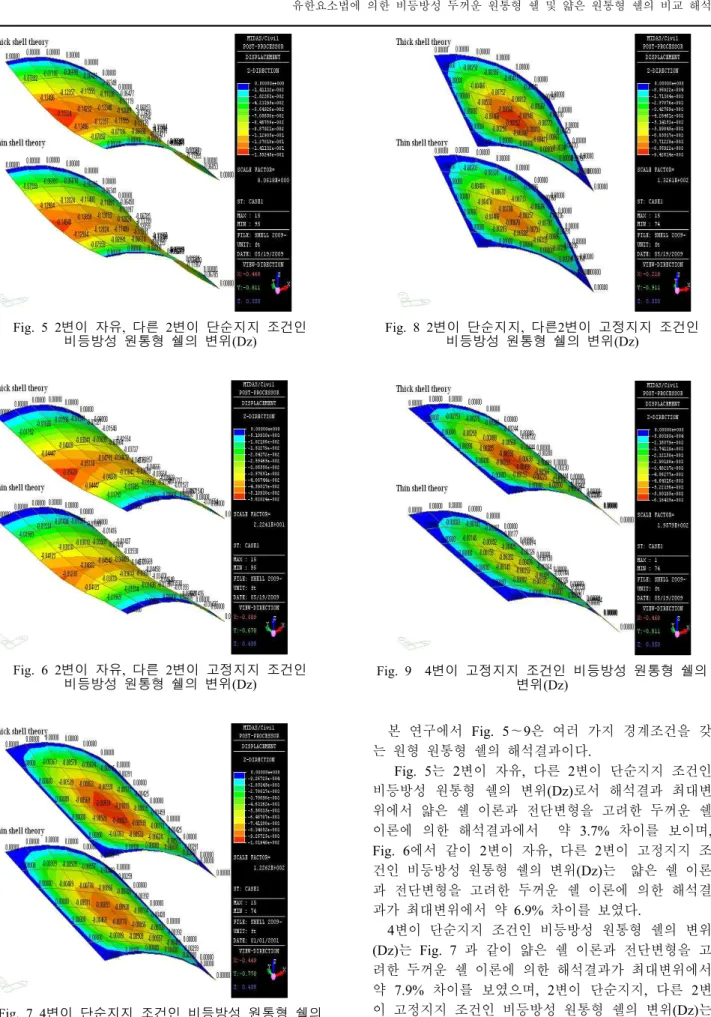
Fig. 5 2변이 자유, 다른 2변이 단순지지 조건인 비등방성 원통형 쉘의 변위(Dz)
Fig. 6 2변이 자유, 다른 2변이 고정지지 조건인 비등방성 원통형 쉘의 변위(Dz)
Fig. 7 4변이 단순지지 조건인 비등방성 원통형 쉘의 변위(Dz)
Fig. 8 2변이 단순지지, 다른2변이 고정지지 조건인 비등방성 원통형 쉘의 변위(Dz)
Fig. 9 4변이 고정지지 조건인 비등방성 원통형 쉘의 변위(Dz)
본 연구에서 Fig. 5∼9은 여러 가지 경계조건을 갖 는 원형 원통형 쉘의 해석결과이다.
Fig. 5는 2변이 자유, 다른 2변이 단순지지 조건인 비등방성 원통형 쉘의 변위(Dz)로서 해석결과 최대변 위에서 얇은 쉘 이론과 전단변형을 고려한 두꺼운 쉘 이론에 의한 해석결과에서 약 3.7% 차이를 보이며, Fig. 6에서 같이 2변이 자유, 다른 2변이 고정지지 조 건인 비등방성 원통형 쉘의 변위(Dz)는 얇은 쉘 이론 과 전단변형을 고려한 두꺼운 쉘 이론에 의한 해석결 과가 최대변위에서 약 6.9% 차이를 보였다.
4변이 단순지지 조건인 비등방성 원통형 쉘의 변위 (Dz)는 Fig. 7 과 같이 얇은 쉘 이론과 전단변형을 고 려한 두꺼운 쉘 이론에 의한 해석결과가 최대변위에서 약 7.9% 차이를 보였으며, 2변이 단순지지, 다른 2변 이 고정지지 조건인 비등방성 원통형 쉘의 변위(Dz)는 Fig. 8 와 같이 얇은 쉘 이론과 전단변형을 고려한 두
꺼운 쉘 이론에 의한 해석결과가 최대변위에서 약 9.1% 차이를 보이고 있으며, 4변이 고정지지 조건인 비등방성 원통형 쉘의 변위(Dz)는 Fig. 9와 같이 얇은 쉘 이론과 전단변형을 고려한 두꺼운 쉘 이론에 의한 해석결과에서는 최대변위가 약 25.4% 차이를 보였다.
4. 결 론
본 연구는 비등방성 재료로 구성되고, 여러 가지 경 계조건을 갖는 원통형 쉘의 거동을 분석하였다. 비등 방성 원통형 쉘에서 얇은 쉘 이론과 두꺼운 쉘이론에 의한 쉘의 폭-두께비에 따른 해석결과에서 폭-두께비가 0.02이상에서 최대 처짐이 약 13.2%이상의 차이를 보 이고 있어, 폭-두께비가 0.02이상의 쉘의 해석에서는 두꺼운 쉘이론을 적용하는 것이 보다 정확한 해석결과 를 얻을 수 있다.
경계조건에 따른 해석결과에서 4변이 고정지지 조건 인 비등방성 원통형 쉘에서 얇은 쉘 이론과 두꺼운 쉘 이론에 의한 쉘의 최대 변위값(Dz)에서 약 25.4%의 최 대 차이를 보였으며, 2변이 자유, 다른 2변이 단순지 지 조건인 비등방성 원통형 쉘의 최대 변위값(Dz)에서 약 3.7%의 최소 차이를 보였다. 또한 원통형 쉘의 변 위값이 등방성 재질보다는 비등방성 재질로 구성된 경 우에 휠씬 전단변형효과의 영향이 커짐을 알 수 있다.
다양한 경계조건과 재질이 비등방성으로 구성된 쉘의 경우 전단변형효과를 고려한 본 논문에서 제시한 두꺼 운 쉘이론을 적용하는 것이 더 정확한 해를 기대할 수 있으며, 따라서 비등방성 원통형 쉘구조물의 해석 및 설계에 본 연구에서의 해석기법이 적용될 수 있을 것 으로 보며, 얇은 쉘 이론과 두꺼운 쉘이론에 의한 비 등방성 얇은 원통형 쉘과 비등방성 두꺼운 원통형 쉘 해석에서 사용되는 유한요소법에 의한 이론적 해석과 정을 명확한 밝힘으로서 설계자들에게 이해를 돕는데 기여할 것으로 본다.
참고 문헌
1. 장석윤, 윤석호(1992) 전단변형을 고려한 비등방성 대칭적층 구형판의 해석, 한국강구조학회논문집 제4 권 제2호, pp187-199.
2. 장석윤, 이원홍(1992) 전단변형을 고려한 주변고정 비등방성 대칭적층 원형판의 해석, 한국강구조학회 논문집 제4권 제1호, pp143-154.
3. 강영주외 57인(2003) M idas Civil User's M anual Volume Ⅲ(Version 6.1.1), MIDAS Inform ation Technology Co., Ltd.
4. Eduard Ventsel Theodor Krauthammer(2001) Thin Plates and Shells, M arcel Dekker, Inc. pp.411-pp421.
Analyses of Plates and Shells, Springer_Verlag Berlin Heidelberg Company, Inc., pp.125-pp210.
7. J. N. Reddy(1981) Mechanics of Laminated Composite shells, CRC press.
8. J. N. Reddy(1995) Energy and Variational M ethods in Applied M echanics, John W illy & Sons, New York, pp.233-247.
9. Robert M . Jones(1975) M echanics of Composite Materials, M cGraw-Hill.
10. Stephen P. Timoshenko & S. Woinowsky-Krieger (1959) Theory of Plates and Shells, M cGraw-Hill 2nd Ed., pp.118-120.
11. Wilhelm Flugge(1973) Stresses in Shells, Springer -Verlag New York Heidelberg Berlin, pp.204-pp235.