Vol. 66, No. 6, June 2016, pp. 734∼741 http://dx.doi.org/10.3938/NPSM.66.734
Hyperbolic Geometry of Relativistically Accelerating Systems
Won Sik L’Yi
∗Department of Physics, Chungbuk National University, Cheongju 28644, Korea (Received 25 March 2015: revised 12 April 2016 : accepted 12 April 2016)
In this paper the hyperbolic geometry is used to investigate geometries of a constantly accerelating observer in the special relativity. The hyperbolic geometry is shown to have properties very similar to those of the Euclidean geometry, so many theorems for Euclidean space have counterparts with almost the same forms in hyperboilc geometry. By using the hyperbolic geometry for the flat Minkowski space, one may investigate a geometric structure of special relativity. As an example of an application of hyperbolic geometry, we investigated the geometric structure of an accerelating observer who travels in space. In addition, the relativistic time dilation and length contraction are explained by using the hyperbolic geometry. The spacetime structure of general relativity is locally flat, which is the same as that of the special relativity, which means that this kind of hyperbolic geometry can be used for general relativity.
PACS numbers: 03.30.+p
Keywords: Special relativity, Hyperbolic geometry
상대론적으로 가속하는 계의 쌍곡기하학
이원식
∗충북대학교 물리학과, 청주 28644, 대한민국
(2016년 3월 25일 받음, 2016년 4월 12일 수정본 받음, 2016년 4월 12일 게재 확정)
본 연구에서는 상대론적으로 일정하게 가속하는 계의 기하학적 특성을 쌍곡기하학이란 관점에서 연 구하였다. 쌍곡기하학은 유클리드 기하학과 매우 유사한 성격을 가지고 있어서 유클리드 기하학의 많은 정리들이 거의 같은 형태로 존재함을 알 수 있었다. 평평한 밍코브스키 공간에서 쌍곡기하학을 적절히 쓰면 특수상대성 이론의 기하학적인 구조를 살펴볼 수 있다. 쌍곡기하학의 응용의 예로서 우주로의 가속 여행의 기하학적인 구조를 설명하였다. 아울러 상대론적인 길이의 수축이나 시간의 팽창을 쌍곡기하학적인 관점에서 살펴보았다. 일반상대성 이론으로 볼 때 시공간은 국소적으로는 특수상대론의 기하학적 구조를 그대로 가지고 있으므로 쌍곡기하학적 방법론은 일반상대론에서도 유용하게 적용될 수 있다.
PACS numbers: 03.30.+p Keywords: 특수상대론, 쌍곡기하학
∗E-mail: wslyi@chungbuk.ac.kr
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
론적인 시공간 구조를 이해하는 실마리를 얻을 수 있다.
본 연구에서는 이 가속계에 관한 연구를 시공간의 쌍곡기 하학적 구조로 살펴봄으로서 기하학적으로 연구하려 한다.
이를 위해 이차원 평면에서의 쌍곡기하학과 불변 거리 및 쌍곡각도를 사용한다. 유클리드 기하학에서는 원점에서 떨어진 길이가 일정한 점들은 원을 이루므로 평면에서 길 이의 비교가 필요할 때는 좌표를 거리와 각도로 표현하는 극좌표계를 사용하는 것이 편리한데, 이와 마찬가지로 밍코 브스키 공간에서는 쌍곡기하학을 사용하는 것이 편리하다.
쌍곡기하학의 특징들은 잘 알려져 있지 않기 때문에 이해 의 첫 걸음을 내딛기 위해 유클리드 공간에서 원이 가지고 있는 성질들은 살펴보고, 이것들이 쌍곡기하학에서는 어떤 유사한 형태의 성질이 있는지 살펴본다.
II 절에서는 가속하는 계를 쌍곡기하학 입장에서 살펴본 다. 유클리드 공간에서 등가속 원운동을 할 경우 극좌표를 사용하면 편리하게 기술할 수 있는데, 이와 유사하게 특수상 대성 이론에서는 불변 반경과 쌍곡각도를 도입하면 편리하 다. 실제로 유클리드 공간에서 등가속 원운동의 가속도 a 는 원운동의 반경 r 과 속력 v 로 a = v2/r과 같이 나타내지는 것처럼, 특수상대론의 시공간 평면에서 등가속도 운동의 가속도는 불변길이 r 로 부터 a = c2/r과 같이 표현된다.
III 절에서는 원운동과 쌍곡선 운동을 비교한다. 원에서 임의의 한 점에서 접선이 가지는 성격을 쌍곡선에서 접선이 가지는 성격과 비교한다. 또 원에서 장반경과 호가 가지는 성격의 쌍곡기하적 꼴을 살펴보고, 원을 두 기준점에 대한 거리의 비로 만들 수 있듯이 쌍곡선도 두 점에 대한 거리의 비로 구성해 본다.
IV 절에서는 쌍곡기하학의 간단한 예로서 우주로의 가속 여행의 쌍곡기하학적인 구조를 살펴보고, 아울러 상대론적 인 길이의 수축과 시간의 팽창도 쌍곡기하학적인 입장에서 다시 설명한다.
II. 가속하는 계와 쌍곡기하학
어떤 관성계O 의 좌표를 (t, x)라 하고, 여기에 대해 가속 하는 관성계O′의 좌표를 (t′, x′)라 두자. 그리고 가속하는
있는 관측자의 고유시간이며, 빛 속도는 편의상 c = 1 로 두었다. 이 식을 사용하여 가속계의 속도 v 를 가속계의 고유시간 τ 에 대하서 풀면
v = tanh aτ (2)
가 된다.
한편 v = dx/dt 이고 dt = γdτ 이므로 (2) 로부터 가속 계의 위치 x(τ ) 는
x(τ ) = 1
acosh aτ (3) 이 된다. 이 식에서 적분상수는 중요하지 않으므로 버렸다.
이제 dt/dτ = 1/√
1− v2의 속도 v 를 (2) 에서 구한 값으로 대입한 후 이를 적분하면
t(τ ) = 1
asinh aτ (4) 을 얻는다 [8].
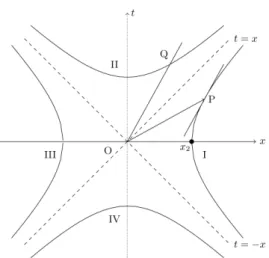
결국 (3) 와 (4) 에서 매개변수인 고유시간 τ 를 소거하면 일정하게 가속하는 계는 관측자O 에서 볼 때 다음과 같은 시간같은 (timelike) 쌍곡선으로 표현된다.1
x2− t2= 1
a2. (5)
이 식의 점근식은 x =±t 로서 좌표계의 원점에서 출발한 빛의 전파를 나타낸다.
식 (3) 과 (4) 에 의하면 가속계의 관측자는 t = 0 순간에 x = 1/a에서 출발하여 원점에서 방출된 빛을 따라잡는데, 출발점 x 가 빛이 방출되는 원점에 가까울수록 요구되는 가속도 a = c2/x는 커야함을 알 수 있다.
이 쌍곡선 (5) 과 짝을 이루는
t2− x2= 1/a2 (6) 는 공간같은 (spacelike) 쌍곡선이 된다. Fig. 1에서와 같이, 본래의 시간같은 쌍곡선 (5) 위의 한 점 P = (t0, x0)과 공
1여기서 시간같은 쌍곡선이란 쌍곡선의 모든 접선이 시간같다는 뜻이며, 공간같은 쌍곡선에 대해서도 대응되는 표현을 쓴다.
Fig. 1. Hyperbolic curve I represents the world line of an accelerating observer who passes through the coordinates (0, x2) of an inertial observerO. The acceleration a when written in terms of the x axis cut x2is x2= 1/a. For an event Q which is symmetric to P relative to t = x line, the instantaneous time axis at P is parallel to OQ. That is, OP and OQ are Lorentz perpendicular. In this sense, hyperbolic curve I is the time axis of an accelerating ob- server, whereas hyperbolic curve II is the corresponding space axis. Hyperbolic curve III represents the world line of an accelerating observer with acceleration −a, while IV represents the corresponding space axis.
간같은 쌍곡선 (6) 위의 한 점 Q = (x0, t0)은 일대일 대응 된다. 특히 O를 좌표의 원점을 나타내고 OP 벡터는 O에서 시작하여 P에서 끝나는 벡터를 의미하고, OQ 벡터도 그런 의미의 벡터라할 때, P에서의 접선은 OQ 벡터와 평행하고, Q에서의 접선은 OP 벡터와 평행하다.
밍코브스키 공간에 로렌쯔 불변길이는 s2= t2− x2로서 좌표의 평행이동에 대해 불변이다. 만일 s2 이 양의 값을 가질 때는 매개변수 (τ, ϑ) 를 도입하여
t = ±τ cosh ϑ, (7)
x = ±τ sinh ϑ (8)
와 같이 나타낼 수 있다. 그리고 만일 s2이 음의 값을 가질 때는 매개변수 (σ, ϑ) 를 도입하여
x = ±σ cosh ϑ, (9)
t = ±σ sinh ϑ. (10)
와 같이 나타낼 수 있는데, 여기서 편의상 ϑ를 쌍곡각도라 하 고 τ 혹은 σ 를 쌍곡반경이라 하자. 이런 매개변수를 도입하 면 밍코브스키 공간의 미소 불변 길이는 ds2= dτ2−τ2dϑ2 혹은 ds2 =−dσ2+ σ2dϑ2와 같이 된다. 시간같은 쌍곡반 경의 경우, 쌍곡각도는 Bondi-factor와 관련이 있다 [9].
특히 등가속하는 관측자의 경우, 쌍곡반경은 σ = 1/a 로 일정하므로 ds2=−dσ2+ σ2dϑ2는 ds2= 1/a2dϑ2,혹은 이를 적분하면 ϑ = as 이다. 여기서 로렌츠 불변 시간 s 는 등가속하는 관측자의 고유시간이기도 하다.
Fig. 2. When the tangent line of a timelike hyperbolic curve at P(t0, x0) meets the x axis at Q(0, x1), and when the hyperbolic curve meets the x axis at R(0, x2), then x0x1 = x22 holds. The Lorentz invariant length of OP is equal to the Lorentz invariant length of OR, that is, x2= σ.
III. 원운동과 쌍곡선 운동의 비교
이차원 유클리드 공간에서 유용한 좌표계는 데카르트 좌표계 (x, y) 와 극좌표계 (r, θ) 인데, 극좌표계는 좌표의 원점에 대해서 등방성을 가지고 있는 계, 예를들어 원운 동을 하는 계의 경우에 편리하다. 이와 유사하게 이차원 밍코브스키 공간에서는 (t, x) 가 기본적으로 사용되지만, 등가속 운동을 하는 계의 경우에서는 쌍곡극좌표계 (τ, ϑ) 혹은 (σ, ϑ) 이 편리하다.
이제부터 유클리드 공간에서 등방성과 밀접한 관련이 있는 이러한 원들이 가지고 성격들과 밍코브스키 공간에서 등가속계와 밀접한 관련이 있는 쌍곡선들의 기하학적 구조 를 비교하여 살펴보자.
1. 접선과 절편에 관한 정리
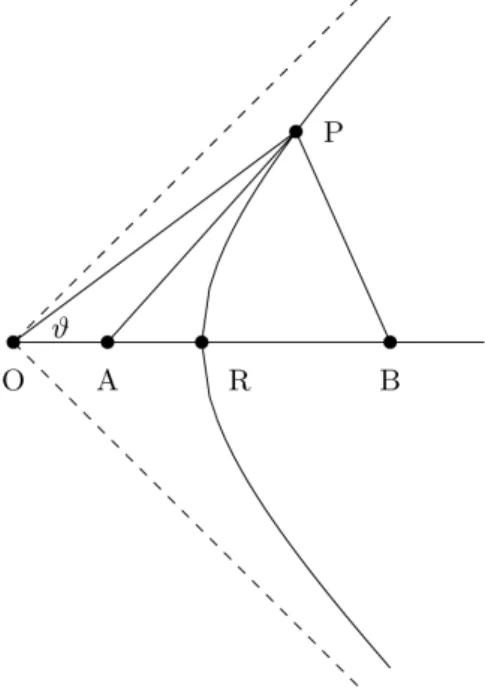
Fig. 2에서 표현한 것과 같이, 일정하게 가속하는 계를 나타내는 시간같은 쌍곡선 (5) 위의 한 점 P(t0, x0)에서의 접선은 가속계의 순간적 시간 축을 나타낸다. 이 접선의 기울기는 (5) 에서부터 dt/dx|0= x0/t0이 되고, 이 접선을 묘사하는 방정식은
t = x0
t0(x− x0) + t0 (11)
Fig. 3. When the center of a circle of radius a is at the origin of the coordinate system, and the tangent line of the circle at P cuts the x axis at x1, then x0x1 = a2, where x0represents the x coordinate of P. On the other hand, OP and QP are perpendicular, and the length QP is euqal to a tan θ0. The relation θ0= θ1also holds.
이 된다. 특히 t = 0 인 지점에서의 x 좌표를 x1이라 할 때, x20− t20= σ2를 사용하면
x1x0= σ2 (12)
를 얻는다. 이것은 Fig. 3에서와 같이 원에서도 똑같은 형 태의 관계식이 존재한다.
한편 Fig. 2에 따르면 x0= σ cosh ϑ0인데, 이를 (12) 에 대입하면 다음과 같은 식을 얻는다.
σ = x1cosh ϑ0. (13) 그리고 Q(0, x1)에서 P(t0, x0)까지의 불변길이를 τ∗라 하면 t20− (x0− x1)2= τ∗2인데, 이를 정리하면
σ2− τ∗2= x21 이 된다2. 이 식에 (13) 를 사용하면
τ∗= x1sinh ϑ0 (14) 를 얻고, 이를 다시 (13) 에 적용하면 다음과 같은 관계식을 얻는다.
τ∗= σ tanh ϑ0. (15)
2 시간 같은 불변의 길이는 기본적으로 τ 를 사용하지만 본 논문에서는 가속계에 있는 관측자의 고유시간을 τ 라고 표현하는 것을 기본으로 고려하기 때문에 지금과 같은 등속운동 관측자의 고유시간은 τ∗로 표현하였다.
Fig. 4. The two hyperbolic curve pairs H+and H−meet the axis at R and L respectively. For a point P on a hyperbolic curve, LP is a timelike vector and RP is a spacelike vector, and they are perpendicular. Further- more, LP2− RP2= (2σ)2holds, where σ is the invariant radius of th hyperbolic curve.
이 세 개의 관계식 (13)–(15) 은 원점 O에서 P를 이은 직선과 P에서의 접선이 서로 밍코브스키 직교하기 때문에 성립한다.
이 직교성은 다음과 같은 방법으로 확인할 수 있다. 즉 좌표의 원점 O에서 쌍곡선의 한 점 P까지의 위치벡터를 OP라 하고, O에서 Q까지의 벡터를 OQ라 하자. 그러면 Q 에서 P까지의 벡터는 QP = (t0, x0− x1)이다. 그러므로
OP· QP = t20− x20+ x0x1
= −σ2+ x0x1
= 0 (16)
이 성립한다.
뿐만 아니라 Q 에서 t 축과 QP를 이은 직선 사이의 쌍곡 각도를 ϑ1이라 하면 t0 = σ sinh ϑ0와 t0 = τ∗cosh ϑ1 이 성립하고, 그러므로 (15) 에서부터
ϑ1= ϑ0 (17)
가 성립한다.
이러한 사실들은 Fig. 3 에서 보는바와 같이 유클리드 기하학에서도 해당되는 형태가 존재함을 알 수 있다.
2. 장반경과 호에 관한 정리
Fig. 4에서 처럼, 시간같은 쌍곡선 x2− t2= σ2은 x > 0 인 H+ 부분과 x < 0 인 H− 부분으로 나뉘어진다. 이 두
Fig. 5. The straight line which passes through the center of a circle of radius a meets the circle at L and R. For a given point P on a circle, LP and RP are perpendicular, and LP2+ RP2= (2a)2.
쌍곡선 부분들이 x 축과 만나는 지점을 각각 L = (−σ, 0)와 R = (σ, 0) 라 하고, 쌍곡선 위의 임의의 한 점을 P = (t0, x0) 라 하자. 그리고 점 L에서 점 P까지 가는 로렌츠 벡터를 LP 라 하고, LP 의 로렌츠 불변길이를 LP 라 하자. 같은 방법으로 RP와 RP 를 정의하자. 그러면 LP = (t0, x0+ σ) 이고 RP = (t0, x0− σ) 이므로 LP · RP = 0 임을 알 수 있다. 특히 LP2− RP2 = (2σ)2 도 성립함을 확인할 수 있다. 여기서 RP2앞의 음의 부호는 RP 벡터가 시간같은 벡터이기 때문이다.
Fig. 5에서 보는바와 같이 이와 유사한 사실이 유클리드 기하학에서도 알려져 있다.
3. 거리의 비로 쌍곡선 만들기
밍코브스키 공간에서 쌍곡선의 성격을 알아보기 전에 우선 Fig. 6과 같이 유클리드 평면에 있는 두 고정점 A와 B를 택하고, 또 어떤 양의 상수 k 를 선택하자. 그리고 평 면에 있는 점 P에 대해서 BP/AP = k 로 일정하다 하자.
그러면 이런 점 P가 그리는 곡선은 유클리드 기하학에서는 원이라는 것이 잘 알려져 있다. 그리고 이떄
OA : OR : OB = 1 : k : k2 (18) 이 성립한다.
이러한 사실은 쌍곡기하학에서도 성립하는데, 다음과 같이 증명이 가능하다. Fig. 7에서와 같이 우선 두 점 A 와 B를 잇는 직선상에서 A보다 왼쪽에 점 O를 택하는데, 단 OB/OA = k2라 하자. 그러면 벡터 AB는 (k2− 1)OA 이다. 그리고 OA + AP = OP = OB + BP = k2OA + BP 이다.
Fig. 6. For given two points A and B in a Euclidean plane and for any given constant k, all the points P which satisfy BP = kAP form a circle. For the center O of this circle, the relation OA : OR : OB = 1 : k : k2 holds.
Fig. 7. For given two points A and B in a Minkowski space, all the points P which satisfy BP = kAP form a hyperbolic curve. The relation OA : OR : OB = 1 : k : k2 holds.
한편 PAB 사이의 쌍곡각도∠PAB를 ϑ라 하면
OP2= OA2+ AP2+ 2OA· AP cosh ϑ (19) 이 된다. 그림에서 보는바와 같이 BP = AP− (k2− 1)OA 이므로
BP2= AP2−2(k2−1)AP·OA cosh ϑ+(k2−1)2OA2 (20) 이다.
점 P를 구성하는 본래의 정의에 의해 BP = kAP 이므로 (20) 을 정리하면
2AP· OA cosh ϑ = (k2− 1)OA2− AP2 (21)
Fig. 8. For Lorentz vectors, the second cosine law such as
|c|2=|a|2+|b|2+ 2|a||b| cosh ϑ is satisfied. In this case, the angle between two vectors is the hyperbolic angle, and the magnitudes of vectors are the Lorentz invariant lengths.
를 얻는다. 이 사실을 (19) 에 대입하면 원점 O에서 P점까 지의 쌍곡거리는
OP = kOA (22)
로서 일정하다. 그리고 아울러
OA : OR : OB = 1 : k : k2 (23) 도 얻는다. 이미 언급한 것과 마찬가지로 이러한 사실은 유클리드 기하학에서 잘 알려져 있다.
4. Cosh 제2법칙
Fig. 8와 같이, 두 벡터 a 와 b 를 공간같은 벡터들이라 하고 이들 사이의 각도를 ϑ 라 하자. 그리고 c 를 이 두 벡터 의 합이라 하자. 그러면 b 의 a 방향 성분은 |b| cosh ϑ 이고 a에 직각 방향 성분은|b| sinh ϑ 이므로 그림에서와 같이 그림에서와 같이
|c|2 = (|a| + |b| cosh ϑ)2− |b|2sinh2ϑ
= |a|2+|b|2+ 2|a||b| cosh ϑ (24) 가 된다. 이것은 유클리드 기하학에서는 cosine 제2법칙으 로 알려져 있다.
IV. 쌍곡기하학의 간단한 응용
일반상대성 이론과 특수상대성 이론은 모두 기하학적 용어로 서술이 된다. 그러므로 이 이론을 기하학적으로 이해하는 것은 매우 중요하다. 지금까지 다뤄 온 밍코브
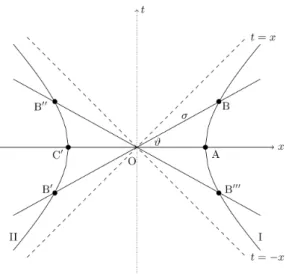
Fig. 9. The hyperbolic curve I represents a positively ac- celerating system, and the hyperbolic curve II represents a negatively accelerating system. They have the same magnitudes of acceleration. The tangents at B and B′ are the same. It means that when one moves curve II to I joining B and B′, the two curves are joined smoothly.
The segment B′′′–A–B/B′–C′–B′′ represents the world line of the space traveler.
스키 공간의 쌍곡기하학적인 성질은 상대성 이론을 기하 학적으로 이해하는데 많은 도움을 줄 것이다. 그 예로서 다음과 같이 우주로의 가속여행을 쌍곡기하학의 특성으로 설명하고, 또 상대론적인 길이의 수축이나 시간의 팽창도 쌍곡기하학으로 이해해보자.
1. 우주로의 가속 여행
어떤 관측자가 지점 A에서부터 지점 C까지 가속 여행을 하는데, 정지상태에서 A에서 출발한 후 A와 C의 중간 지점 인 B까지는 +a 로 가속하고 B에서 C까지는−a로 감속하 여 C에 정지한다고 하자. 그리한 후, 다시 C에서 A까지는 이와 유사하게 가속과 감속을 교대하여 A에 도착한다고 하자. [8]
이것은 Fig. 9와 같은 그림으로 나타낼 수 있다. 그림의 B 에서 접선의 기울기는 B′에서의 접선의 기울기와 같으므로 쌍곡선 II를 옮겨 B′이 B에 놓이게 하면 세계선은 부드럽게 연결된다. 또 A에서 B까지의 운동은 가속운동이고, B′에서 B′′까지의 운동은 같은 크기의 감속 운동이다. 마지막으로 B′′′에서 A까지의 운동은 같은 크기의 가속운동이다.
정지한 좌표계가 본 A에서 B까지의 시간 tAB과 가속계 안에 있는 관측자의 고유시간 τAB을 비교해 보자. OB의 불변거리를 σ 라 하면 τAB = σϑ = ϑ/a이다. 이를 사용하 면 tAB= σ sinh ϑ에서
tAB =1
asinh(aτAB) (25)
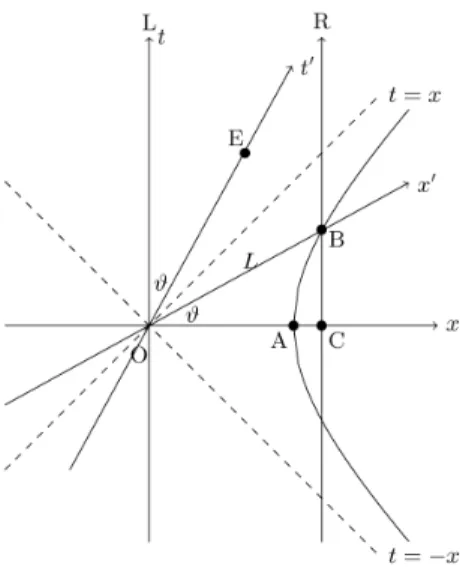
Fig. 10. When one measures a ruler of rest length L0 = OC in a moving coordinate system (t′, x′), one needs to measure both ends of the ruler simultaneously. All the events on the x′ axis have the same t′, and the distance L between O and B is the length of the ruler measured in the moving inertial coordinate system. It is clear that OB = OA is less than OC. That is, the length contract.
In addition to this, L cosh ϑ = L0 implies L = L0/γ.
를 얻는다.
우주 왕복 여행에 필요한 총 시간은 각각 t = 4tAB와 τ = 4τAB이므로 결국
t = 4
asinh(aτ
4 ) (26)
를 얻는다.
2. 길이의 수축과 시간의 팽창
이제 상대론적인 길이의 수축과 시간의 팽창을 쌍곡기하 학적인 관점에서 살펴보자.
1) 길이의 수축
정지상태에서 길이가 L0인 막대의 왼쪽이 x = 0 에 놓여 있고 오른쪽은 x = L0 에 놓어있다 하자. 이때 이 막대를 이 관측자에 대해서 속도 v 로 움직이는 관측자가 측정한 길이를 쌍곡기하학으로 계산해보자.
Fig. 10에서 막대의 왼쪽 끝과 오른쪽 끝을 나타내는 두 개의 세계선은 각각 L과 R로 표현되어 있고, 이 세계선들이 x과 만나는 간격은 막대의 길이 OC = L0이다.
이 관성계에 대해서 상대속도 v 로 움직이는 관성계 (t′, x′) 의 경우, 이 관성계의 원점에 있는 관측자의 움직임을 나타
Fig. 11. The time t′E= OE measured by a moving clock at the origin of moving coordinates (t′, x′), and the time tE measured by a clock at rest in the rest coordinate system (t, x) satisfies tE= t′Ecosh ϑ = γt′E.
내는 세계선은 좌표축 t′과 동일하다. 그러므로 t′축에 놓인 관측자의 두 순간, 예를 들어 사건 O와 사건 E를 정지된 좌표계에서 관측하면 움직이는 관측자의 속도를 구할 수 있다. 그 속도는 다음과 같다.
v = xE tE
= tanh ϑ. (27) 한편 움직이는 좌표계 (t′, x′)에서 x′축 상에 있는 모든 점은 이 움직이는 좌표계에서 t′ = 0으로 동시이고, 그래서 움직이는 좌표계에서 측정한 이 막대의 길이는 두 세계선과 x′축이 만나는 길이 OB = L 이다.
원점에서 로렌츠 불변 길이가 L 인 곡선은 B를 지나는 쌍곡선을 이루므로 이 쌍곡선이 x 축과 만나는 점을 A라 할 때 L = OA < OC = L0 인 것을 알 수 있다. 즉 막대가 움직일 때 길이를 측정하면 길이는 수축됨을 알수 있다.
특히 OB cosh ϑ = OC 이므로 L = L0/ cosh ϑ = L/γ이다.
여기서 γ = 1/√
1− v2이다.
2) 시간의 팽창
속도 v 로 움직이는 좌표계 (t′, x′)의 원점에 놓인 시계가 가르키는 시간이 t′E라 해보자. 이 시간을 정지된 좌표계에서 측정하면 Fig. 11의 tE와 같은데, 이것은 분명히 OA = t′E 보다 크다. 즉 사건이 움직이면서 일어나면 시간은 고유시 간보다 늘어나는 것을 알 수 있다.
고유시간 t′E를 τ 라 하고 t = tE 라 두면 t = τ cosh ϑ
= γτ (28)
와 같이 되고, 이것은 시간의 팽창으로 알려져 있다.
Fig. 12. The line segments a and b in a Minkowski space are orthogonal, and the length of the spacelike hy- potenuse c satisfies a = c cosh ϑ and b = c sinh ϑ, where ϑ is the hyperbolic angle between the two spacelike seg- ments a and c.
V. 결 론
아인슈타인의 일반성대성 이론의 중력장 방정식은 4차원 기하학적인 양과 물리적인 양의 동등성으로 표현되어진다.
즉 일반상대성 이론은 기본적으로 기하학적인 기초에 세워 져 있다고 할 수 있다. 그리고 일반상대성 이론의 특수한 경우인 특수상대성 이론도 그 뿌리에는 기하학적인 구조가 있다. 그러므로 상대성이론을 근본적으로 기하학적으로 이해하는 것은 매주 중요하다.
유클리드 기하학에서 보듯이 기학학에서 불변의 길이와 각도란 개념은 기본적이다. 특히 길이가 일정한 점을 이은 도형인 원이 가지고 있는 성격을 잘 이해하는 것은 유클리드 기하학에서 중요하다. 이와 마찬가지로 잉코브스키 공간 에서 길이가 일정한 점들을 이은 도형인 쌍곡선이 가지는 성격들을 잘 알아두는 것이 상대성 이론의 기하학적인 구조 를 이해하는데 중요하다. 본 논문에서는 이 두 기하학에는 유사성이 있어서 원이 가지는 다양한 성질들을 쌍곡선이 가지고 있음으로 보였다. 이러한 연구는 상대론을 기하학 적으로 이해하는데 많은 도움을 준다고 생각되어진다.
감사의 글
이 논문은 2015 년도 충북대학교 학술연구지원사업의 교내연구비 지원에 의하여 연구되었습니다.
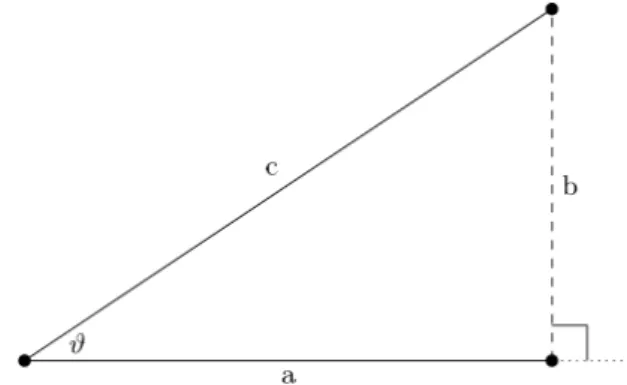
편의상 a와 b는 서로 직교한다고 한다. 그리고 a와 b를 이은 선분 c 는 공간같은 선분이라고 하자. 그러면 a2− b2= c2 이 된다. 특히 두 공간같은 선분 사이의 쌍곡 각도를 ϑ 라 하고 tanh ϑ = v 라 두면
a = c cosh ϑ = γc b = c sinh ϑ = γvc
인데, 여기서 γ = 1/√
1− v2이다. 이러한 사실은 a 와 c 가 시간같고 b 는 공간같을 때도 성립된다.
REFERENCES
[1] A. G. Riess, A. V. Filippenko, P. Challis, A. Cloc- chiatti and A. Diercks et al., Astron. J. 116, 1009 (1998).
[2] S. Perlmutter, G. Aldering, G. Goldhaber, R. A.
Knop and P. Nugent et al., Astrophys. J. 517, 565 (1999).
[3] A. G. Riess, L.-G. Strolger, J. Tonry, S. Casertano and H. C. Ferguson et al., Astrophys. J. 607, 665 (2004).
[4] S. A. Fulling, Phys. Rev. D 7, 2850 (1973).
[5] P. C. W. Davies, J. Phys. A 8, 609 (1975) . [6] W. G. Unruh, Phys. Rev. D 14, 870 (1976).
[7] J. S. Chung, W. S. L’Yi and J. H. Chung, J. Korean Phys. Soc. 55, 2323 (2009).
[8] E. F. Taylor and J. A. Wheeler, Spacetime Physics (W. H. Freeman & Company, 1992).
[9] M. Ludvigsen, General Relativit, A Geometric Ap- proach (Cambridge University Press, 1999), Chap. 3.